Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ures, Raúl
2011.
Intrinsic ergodicity of partially hyperbolic diffeomorphisms with a hyperbolic linear part.
Proceedings of the American Mathematical Society,
Vol. 140,
Issue. 6,
p.
1973.
RODRIGUEZ HERTZ, F.
RODRIGUEZ HERTZ, M. A.
TAHZIBI, A.
and
URES, R.
2012.
Maximizing measures for partially hyperbolic systems with compact center leaves.
Ergodic Theory and Dynamical Systems,
Vol. 32,
Issue. 2,
p.
825.
BUZZI, J.
FISHER, T.
SAMBARINO, M.
and
VÁSQUEZ, C.
2012.
Maximal entropy measures for certain partially hyperbolic, derived from Anosov systems.
Ergodic Theory and Dynamical Systems,
Vol. 32,
Issue. 1,
p.
63.
Potrie, Rafael
2014.
A Few Remarks on Partially Hyperbolic Diffeomorphisms of $${\mathbb T}^3$$ T 3 Isotopic to Anosov.
Journal of Dynamics and Differential Equations,
Vol. 26,
Issue. 3,
p.
805.
Saghin, Radu
2014.
Volume growth and entropy for $C^1$ partially hyperbolic diffeomorphisms.
Discrete & Continuous Dynamical Systems - A,
Vol. 34,
Issue. 9,
p.
3789.
Roldan, Mario
2015.
Hyperbolic sets and entropy at the homological level.
Discrete and Continuous Dynamical Systems,
Vol. 36,
Issue. 6,
p.
3417.
Saghin, Radu
and
Yang, Jiagang
2016.
Continuity of topological entropy for perturbation of time-one maps of hyperbolic flows.
Israel Journal of Mathematics,
Vol. 215,
Issue. 2,
p.
857.
Hu, Huyi
Hua, Yongxia
and
Wu, Weisheng
2017.
Unstable entropies and variational principle for partially hyperbolic diffeomorphisms.
Advances in Mathematics,
Vol. 321,
Issue. ,
p.
31.
Buzzi, Jérôme
Crovisier, Sylvain
and
Fisher, Todd
2018.
The entropy of 𝐶¹-diffeomorphisms without a dominated splitting.
Transactions of the American Mathematical Society,
Vol. 370,
Issue. 9,
p.
6685.
Wang, Lin
Wang, Xin-sheng
and
Zhu, Yu-jun
2018.
On Local Constancy of Topological Entropy for Certain Partially Hyperbolic Diffeomorphisms.
Acta Mathematicae Applicatae Sinica, English Series,
Vol. 34,
Issue. 2,
p.
249.
Ponce, Gabriel
2019.
Unstable entropy of partially hyperbolic diffeomorphisms along non-compact subsets.
Nonlinearity,
Vol. 32,
Issue. 7,
p.
2337.
Crisostomo, J
and
Tahzibi, A
2019.
Equilibrium states for partially hyperbolic diffeomorphisms with hyperbolic linear part.
Nonlinearity,
Vol. 32,
Issue. 2,
p.
584.
Roldán, Mario
Saghin, Radu
and
Yang, Jiagang
2020.
Entropy of partially hyperbolic flows with center dimension two.
Nonlinearity,
Vol. 33,
Issue. 2,
p.
790.
Huang, Ping
Wang, Chenwei
and
Chen, Ercai
2021.
Unstable topological entropy in meanu-metrics for partially hyperbolic systems.
Dynamical Systems,
Vol. 36,
Issue. 3,
p.
387.
Dahinden, Lucas
2021.
C0-stability of topological entropy for contactomorphisms.
Communications in Contemporary Mathematics,
Vol. 23,
Issue. 06,
p.
2150015.
Álvarez, Carlos F.
2021.
Hyperbolic measures for certain dynamics on $$\mathbb {T}^{4}$$.
São Paulo Journal of Mathematical Sciences,
Vol. 15,
Issue. 2,
p.
875.
HU, HUYI
WU, WEISHENG
and
ZHU, YUJUN
2021.
Unstable pressure and u-equilibrium states for partially hyperbolic diffeomorphisms.
Ergodic Theory and Dynamical Systems,
Vol. 41,
Issue. 11,
p.
3336.
Tahzibi, Ali
2021.
Unstable entropy in smooth ergodic theory
*
.
Nonlinearity,
Vol. 34,
Issue. 8,
p.
R75.
Wu, Weisheng
2022.
On the continuity of topological entropy of certain partially hyperbolic diffeomorphisms.
Nonlinearity,
Vol. 35,
Issue. 6,
p.
2695.
Fakhari, Abbas
and
Garakani, Mohammad Khalili
2022.
Uniqueness and Continuity of Equilibrium States for DA-Diffeomorphisms.
Qualitative Theory of Dynamical Systems,
Vol. 21,
Issue. 4,
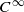 diffeomorphisms. The proof uses a topological invariant we introduced, Yomdin’s theorem on upper semi-continuity, Katok’s theorem on lower semi-continuity for two-dimensional systems, and a refined Pesin–Ruelle inequality we proved for partially hyperbolic diffeomorphisms.
diffeomorphisms. The proof uses a topological invariant we introduced, Yomdin’s theorem on upper semi-continuity, Katok’s theorem on lower semi-continuity for two-dimensional systems, and a refined Pesin–Ruelle inequality we proved for partially hyperbolic diffeomorphisms.
