No CrossRef data available.
Article contents
Topological full groups of minimal subshifts and quantifying local embeddings into finite groups
Part of:
Structure and classification of infinite or finite groups
Topological dynamics
Special aspects of infinite or finite groups
Published online by Cambridge University Press: 05 April 2022
Abstract
We investigate quantitative aspects of the locally embeddable into finite groups (LEF) property for subgroups of the topological full group 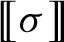 of a two-sided minimal subshift over a finite alphabet, measured via the LEF growth function. We show that the LEF growth of
of a two-sided minimal subshift over a finite alphabet, measured via the LEF growth function. We show that the LEF growth of 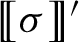 may be bounded from above and below in terms of the recurrence function and the complexity function of the subshift, respectively. As an application, we construct groups of previously unseen LEF growth types, and exhibit a continuum of finitely generated LEF groups which may be distinguished from one another by their LEF growth.
may be bounded from above and below in terms of the recurrence function and the complexity function of the subshift, respectively. As an application, we construct groups of previously unseen LEF growth types, and exhibit a continuum of finitely generated LEF groups which may be distinguished from one another by their LEF growth.
MSC classification
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
Arzhantseva, G. and Cherix, P. A.. Quantifying metric approximations of groups. Preprint, 2020, arXiv:2008.12954 [math.GR].Google Scholar
Bezuglyi, S. and Medynets, K.. Full groups, flip conjugacy, and orbit equivalence of Cantor minimal systems. Colloq. Math. 110(2) (2008), 409–429.CrossRefGoogle Scholar
Bou-Rabee, K., Chen, J. and Timashova, A.. Residual finiteness growths of Lamplighter groups. Preprint, 2019, arXiv:1909.03535 [math.GR].Google Scholar
Bou-Rabee, K. and Studenmund, D.. Full residual finiteness growth of nilpotent groups. Israel J. Math. 214(1) (2016), 209–233.CrossRefGoogle Scholar
Bradford, H.. Quantifying local embeddings into finite groups. Preprint, 2021, arXiv:2104.07111 [math.GR].Google Scholar
Elek, G. and Szabó, E.. On sofic groups. J. Group Theory 9(2) (2006), 161–171.CrossRefGoogle Scholar
Grigorchuk, R. I. and Medynets, K. S.. On algebraic properties of topological full groups. Sb. Math. 205(6) (2014), 843–861.CrossRefGoogle Scholar
Johnson, D. L.. Minimal permutation representations of finite groups. Amer. J. Math. 93(4) (1971), 857–866.CrossRefGoogle Scholar
Jung, U., Lee, J. and Park, K. K.. Constructions of subshifts with positive topological entropy dimension. Preprint, 2016, arXiv:1601.07259v1 [math.DS].Google Scholar
Juschenko, K.. A companion to the mini-course on full topological groups of Cantor minimal systems. https://web.ma.utexas.edu/users/juschenko/files/Juschenko-Course.pdf.Google Scholar
Juschenko, K. and Monod, N.. Cantor systems, piecewise translations and simple amenable groups. Ann. of Math. (2) 178(2) (2013), 775–787.CrossRefGoogle Scholar
Matui, H.. Some remarks on topological full groups of Cantor minimal systems. Internat. J. Math. 17(2) (2006), 231–251.CrossRefGoogle Scholar
Morse, M. and Hedlund, G. A.. Symbolic dynamics. Amer. J. Math. 60(4) (1938), 815–866.CrossRefGoogle Scholar
Morse, M. and Hedlund, G. A.. Symbolic dynamics II. Sturmian trajectories. Amer. J. Math. 62(1) (1940), 1–42.CrossRefGoogle Scholar
Vershik, A. M. and Gordon, E. I.. Groups that are locally embeddable in the class of finite groups. St. Petersburg Math. J. 9(1) (1998), 49–68.Google Scholar


