Hostname: page-component-7dd5485656-tbj44 Total loading time: 0 Render date: 2025-10-31T21:28:21.215Z Has data issue: false hasContentIssue false
  • English
  • Français

Total disconnectedness of Julia sets of random quadratic polynomials

Part of: Complex dynamical systems Two-dimensional theory

Published online by Cambridge University Press:  04 March 2021

KRZYSZTOF LECH  and
ANNA ZDUNIK
KRZYSZTOF LECH
Affiliation:
Institute of Mathematics, University of Warsaw, ul. Banacha 2, 02-097 Warsaw, Poland (e-mail: K.Lech@mimuw.edu.pl)
ANNA ZDUNIK*
Affiliation:
Institute of Mathematics, University of Warsaw, ul. Banacha 2, 02-097 Warsaw, Poland (e-mail: K.Lech@mimuw.edu.pl)
*
e-mail: A.Zdunik@mimuw.edu.pl
Get access Rights & Permissions [Opens in a new window]

Abstract

For a sequence of complex parameters 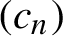$(c_n)$ we consider the composition of functions 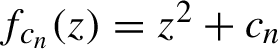$f_{c_n} (z) = z^2 + c_n$, the non-autonomous version of the classical quadratic dynamical system. The definitions of Julia and Fatou sets are naturally generalized to this setting. We answer a question posed by Brück, Büger and Reitz, whether the Julia set for such a sequence is almost always totally disconnected, if the values 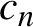$c_n$ are chosen randomly from a large disc. Our proof is easily generalized to answer a lot of other related questions regarding typical connectivity of the random Julia set. In fact we prove the statement for a much larger family of sets than just discs; in particular if one picks 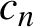$c_n$ randomly from the main cardioid of the Mandelbrot set, then the Julia set is still almost always totally disconnected.

Keywords

random dynamicsholomorphic dynamicsJulia setsconnectivity

MSC classification

Primary: 37F10: Polynomials; rational maps; entire and meromorphic functions
Secondary: 31A05: Harmonic, subharmonic, superharmonic functions

Information

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 5 , May 2022 , pp. 1764 - 1780
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Branner, B. and Hubbard, J. H.. The iteration of cubic polynomials part II: Patterns and parapatterns. Acta Math. 169(3–4) (1992), 229–325.CrossRefGoogle Scholar
Brück, R.. Connectedness and stability of Julia sets of the composition of polynomials of the form ${z}^2+{c}_n$ . J. Lond. Math. Soc. 61 (2000), 462–470.CrossRefGoogle Scholar
Brück, R., Büger, M. and Reitz, S.. Random iteration of polynomials of the form ${z}^2+c$ : connectedness of Julia sets. Ergod. Th. & Dynam. Sys. 19 (1999), 1221–1231.CrossRefGoogle Scholar
Büger, M.. On the composition of polynomials of the form ${z}^2+{c}_n$ . Math. Ann. 310 (1998), 661–683.Google Scholar
Comerford, M.. Hyperbolic non-autonomous Julia sets. Ergod. Th. & Dynam. Sys. 26 (2006), 353–377.CrossRefGoogle Scholar
Comerford, M.. Non-autonomous Julia sets with escaping critical points. J. Difference Equ. Appl. 17 (2011), 1813–1826.CrossRefGoogle Scholar
Fornæss, J. E. and Sibony, N.. Random iterations of rational functions. Ergod. Th. & Dynam. Sys. 11 (1991), 687–708.CrossRefGoogle Scholar
Gong, Z., Qiu, W. and Li, Y.. Connectedness of Julia sets for a quadratic random dynamical system. Ergod. Th. & Dynam. Sys. 23 (2003), 1807–1815.CrossRefGoogle Scholar
Mayer, V., Skorulski, B. and Urbański, M.. Distance Expanding Random Mappings, Thermodynamical Formalism, Gibbs Measures and Fractal Geometry (Lecture Notes in Mathematics, 2036) (Springer, Berlin, 2011).CrossRefGoogle Scholar
McMullen, C. T.. Complex Dynamics and Renormalization (Princeton University Press, Princeton, NJ, 1994).Google Scholar