Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Schmoll, Martin
and
Johnson, Chris
2014.
Pseudo-Anosov eigenfoliations on Panov planes.
Electronic Research Announcements in Mathematical Sciences,
Vol. 21,
Issue. 0,
p.
89.
GUELMAN, NANCY
KOROPECKI, ANDRES
and
TAL, FABIO ARMANDO
2015.
Rotation sets with non-empty interior and transitivity in the universal covering.
Ergodic Theory and Dynamical Systems,
Vol. 35,
Issue. 3,
p.
883.
ADDAS-ZANATA, SALVADOR
and
DE PAULA JACOIA, BRUNO
2021.
A condition that implies full homotopical complexity of orbits for surface homeomorphisms.
Ergodic Theory and Dynamical Systems,
Vol. 41,
Issue. 1,
p.
1.
Bowden, Jonathan
Hensel, Sebastian
Mann, Kathryn
Militon, Emmanuel
and
Webb, Richard
2022.
Rotation sets and actions on curves.
Advances in Mathematics,
Vol. 408,
Issue. ,
p.
108579.

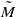 . Roughly speaking, this means that
. Roughly speaking, this means that  have dense leaves. The proof relies on a characterization of transitivity for twisted ℤ
have dense leaves. The proof relies on a characterization of transitivity for twisted ℤ