Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-10T12:25:34.106Z Has data issue: false hasContentIssue false
  • English
  • Français

Unstable pressure and u-equilibrium states for partially hyperbolic diffeomorphisms

Part of: Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  03 November 2020

HUYI HU ,
WEISHENG WU  and
YUJUN ZHU
HUYI HU
Affiliation:
Department of Mathematics, Southern University of Science and Technology of China, Shenzhen, P. R. China (e-mail: huhy@sustc.edu.cn) Department of Applied Mathematics, College of Science, China Agricultural University, Beijing, 100083, P. R. China (e-mail: hhu@math.msu.edu)
WEISHENG WU*
Affiliation:
School of Mathematical Sciences, Xiamen University, Xiamen, 361005, P. R. China (e-mail: yjzhu@xmu.edu.cn)
YUJUN ZHU
Affiliation:
School of Mathematical Sciences, Xiamen University, Xiamen, 361005, P. R. China (e-mail: yjzhu@xmu.edu.cn)
*
e-mail: wuweisheng@cau.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

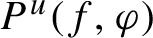Unstable pressure and u-equilibrium states are introduced and investigated for a partially hyperbolic diffeomorphism f. We define the unstable pressure $P^{u}(f, \varphi )$ of f at a continuous function $\varphi $ via the dynamics of f on local unstable leaves. A variational principle for unstable pressure 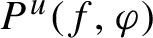$P^{u}(f, \varphi )$ , which states that 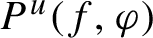$P^{u}(f, \varphi )$ is the supremum of the sum of the unstable entropy and the integral of 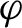$\varphi $ taken over all invariant measures, is obtained. U-equilibrium states at which the supremum in the variational principle attains and their relation to Gibbs u-states are studied. Differentiability properties of unstable pressure, such as tangent functionals, Gateaux differentiability and Fréchet differentiability and their relations to u-equilibrium states, are also considered.

Keywords

Unstable pressureu-equilibrium statepartial hyperbolicity

MSC classification

Primary: 37D35: Thermodynamic formalism, variational principles, equilibrium states
Secondary: 37D30: Partially hyperbolic systems and dominated splittings
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 11 , November 2021 , pp. 3336 - 3362
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

References

Bonatti, C., Díaz, L. J., and Viana, M.. Dynamics Beyond Uniform Hyperbolicity. A Global Geometric and Probabilitistic Perspective (Encyclopaedia of Mathematical Sciences, 102)s. Springer, Berlin, 2005.Google Scholar
Bonatti, C. and Viana, M.. SRB measures for partially hyperbolic systems whose central direction is mostly contracting. Israel J. Math. 115(2000), 157–193.CrossRefGoogle Scholar
Bowen, R.. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms (Lecture Notes in Mathematics, 470). Springer, Berlin, 1975.CrossRefGoogle Scholar
Buzzi, J.. ${C}^r$ surface diffeomorphisms with no maximal entropy measure. Ergod. Th. & Dynam. Sys. 34(6) (2014), 1770–1793.CrossRefGoogle Scholar
Downarowicz, T.. Entropy in Dynamical Systems (New Mathematical Monographs, 18). Cambridge University Press, Cambridge 2011.CrossRefGoogle Scholar
Dunford, N. and Schwartz, J. T.. Linear Operators Part I: General Theory. Interscience, New York, NY, 1958.Google Scholar
Grayson, M., Pugh, C., and Shub, M.. Stably ergodic diffeomorphisms. Ann. of Math. (2) 140(1994), 295–329.CrossRefGoogle Scholar
Hirsch, M. W., Pugh, C. C. and Shub, M.. Invariant manifolds. Bull. Amer. Math. Soc. 76(5) (1970), 1015–1019.CrossRefGoogle Scholar
Hu, H., Hua, Y., and Wu, W.. Unstable entropies and variational principle for partially hyperbolic diffeomorphisms. Adv. Math. 321(2017), 31–68.CrossRefGoogle Scholar
Hua, Y., Saghin, R., and Xia, Z.. Topological entropy and partially hyperbolic diffeomorphisms. Ergod. Th. & Dynam. Sys. 28(3) (2008), 843–862.CrossRefGoogle Scholar
Ledrappier, F. and Young, L.-S.. The metric entropy of diffeomorphisms: part II: relations between entropy, exponents and dimension. Ann. Math. 122(3) (1985), 540–574.CrossRefGoogle Scholar
Misiurewicz, M.. Diffeomorphism without any measure of maximal entropy. Bull. Acad. Pol. Sci. 21(1973), 903–910.Google Scholar
Pesin, Ya. B.. Dimension Theory in Dynamical Systems: Contemporary Views and Applications (Chicago Lectures in Mathematics). University of Chicago Press, Chicago, IL, 2008.Google Scholar
Pesin, Ya. B., and Sinai, Ya. G.. Gibbs measures for partially hyperbolic attractors. Ergod. Th. & Dynam. Sys. 2(3–4) (1982), 417–438.CrossRefGoogle Scholar
Ponce, G.. Unstable entropy of partially hyperbolic diffeomorphisms along non-compact subsets. Nonlinearity 32(7) (2019), 2337–2351.CrossRefGoogle Scholar
Rodriguez Hertz, F., Rodriguez Hertz, M. A., and Ures, R.. Accessibility and stable ergodicity for partially hyperbolic diffeomorphisms with 1d-center bundle. Invent. Math. 172(2) (2008), 353–381.CrossRefGoogle Scholar
Rohlin, V. A.. On the fundamental ideas of measure theory. Amer. Math. Soc. Translations 171 (1952), 55 pp. Engl. Transl. of Mat. Sbornik 25 (1949), 107–150.Google Scholar
Ruelle, D.. Statistical mechanics on a compact set with ${\mathbb{Z}}^{\nu }$ action satisfying expansiveness and specification. Trans. Amer. Math. Soc. 187(1973), 237–251.CrossRefGoogle Scholar
Tian, X. and Wu, W.. Unstable entropies and dimension theory of partially hyperbolic systems. Preprint, 2018, arXiv:1811.03797.Google Scholar
Walters, P.. A variational principle for the pressure of continuous transformations. Amer. J. Math. 97(4) (1975), 937–971.CrossRefGoogle Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79). Springer, New York, NY, 1982.CrossRefGoogle Scholar
Walters, P.. Differentiability properties of the pressure of a continuous transformation on a compact metric space. J. Lond. Math. Soc. 46(3) (1992), 471–481.CrossRefGoogle Scholar
Wang, L. and Zhu, Y.. Center specification property and entropy for partially hyperbolic diffeomorphisms. Discrete Contin. Dyn. Syst. 36(1) (2016), 469–479.CrossRefGoogle Scholar
Yang, J.. Entropy along expanding foliations. Preprint, 2016, arXiv:1601.05504.Google Scholar