Hostname: page-component-7dd5485656-glrdx Total loading time: 0 Render date: 2025-10-31T13:44:14.887Z Has data issue: false hasContentIssue false
  • English
  • Français

A variational principle for the metric mean dimension of free semigroup actions

Part of: Dynamical systems with hyperbolic behavior Special properties Topological dynamics Smooth dynamical systems: general theory

Published online by Cambridge University Press:  01 February 2021

MARIA CARVALHO Open the ORCID record for MARIA CARVALHO [Opens in a new window] ,
FAGNER B. RODRIGUES Open the ORCID record for FAGNER B. RODRIGUES [Opens in a new window]  and
PAULO VARANDAS
MARIA CARVALHO
Affiliation:
CMUP & Departamento de Matemática, Universidade do Porto, Porto, Portugal (e-mail: mpcarval@fc.up.pt)
FAGNER B. RODRIGUES*
Affiliation:
Departamento de Matemática, Universidade Federal do Rio Grande do Sul, Porto Alegre, Brazil
PAULO VARANDAS
Affiliation:
CMUP & Departamento de Matemática e Estatística, Universidade Federal da Bahia, Bahia, Brazil (e-mail: paulo.varandas@ufba.br)
*
e-mail: fagnerbernardini@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider continuous free semigroup actions generated by a family 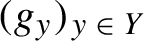$(g_y)_{y \,\in \, Y}$ of continuous endomorphisms of a compact metric space 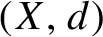$(X,d)$, subject to a random walk 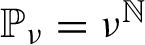$\mathbb P_\nu =\nu ^{\mathbb N}$ defined on a shift space 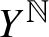$Y^{\mathbb N}$, where 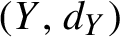$(Y, d_Y)$ is a compact metric space with finite upper box dimension and 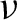$\nu $ is a Borel probability measure on Y. With the aim of elucidating the impact of the random walk on the metric mean dimension, we prove a variational principle which relates the metric mean dimension of the semigroup action with the corresponding notions for the associated skew product and the shift map $\sigma $ on 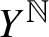$Y^{\mathbb {N}}$, and compare them with the upper box dimension of Y. In particular, we obtain exact formulas whenever 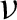$\nu $ is homogeneous and has full support. We also discuss several examples to enlighten the roles of the homogeneity, of the support and of the upper box dimension of the measure 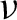$\nu $, and to test the scope of our results.

Keywords

free semigroup actionhomogeneous measuremetric mean dimensionskew productupper box dimension

MSC classification

Primary: 37B05: Transformations and group actions with special properties (minimality, distality, proximality, etc.) 37C45: Dimension theory of dynamical systems 54F45: Dimension theory
Secondary: 37C85: Dynamics of group actions other than ${bf Z}$ and ${bf R}$, and foliations 37D35: Thermodynamic formalism, variational principles, equilibrium states 37B40: Topological entropy

Information

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 1 , January 2022 , pp. 65 - 85
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

Bélair, J. and Dubuc, S., Eds. Fractal Geometry and Analysis (NATO ASI Science Series C, 346). Springer, Netherlands, 1991.CrossRefGoogle Scholar
Biś, A.. An analogue of the variational principle for group and pseudogroup actions. Ann. Inst. Fourier 63(3) (2013), 839–863.CrossRefGoogle Scholar
Bonatti, C., Díaz, L. J. and Viana, M.. Dynamics Beyond Uniform Hyperbolicity (Encyclopaedia of Mathematical Sciences, 102). Springer, Berlin, 2005.Google Scholar
Bufetov, A.. Topological entropy of free semigroup actions and skew-product transformations. J. Dyn. Control Syst. 5 (1999), 137–143.CrossRefGoogle Scholar
Carvalho, M., Rodrigues, F. and Varandas, P.. Semigroup actions of expanding maps. J. Stat. Phys. 116(1) (2017), 114–136.CrossRefGoogle Scholar
Carvalho, M., Rodrigues, F. and Varandas, P.. Quantitative recurrence for free semigroup actions. Nonlinearity 31(3) (2018), 864–886.CrossRefGoogle Scholar
Carvalho, M., Rodrigues, F. and Varandas, P.. A variational principle for free semigroup actions. Adv. Math. 334 (2018), 450–487.CrossRefGoogle Scholar
Carvalho, M., Rodrigues, F. and Varandas, P.. Generic homeomorphisms have full metric mean dimension. Ergod. Th. & Dynam. Sys. https://doi.org/10.1017/etds.2020.130. Published online 28 December 2020.CrossRefGoogle Scholar
Falconer, K.. Fractal Geometry: Mathematical Foundations and Applications. John Wiley & Sons, Chichester, 1990.Google Scholar
Gromov, M.. Topological invariants of dynamical systems and spaces of holomorphic maps I. Math. Phys. Anal. Geom. 2(4) (1999), 323–415.CrossRefGoogle Scholar
Kloeckner, B.. Optimal transport and dynamics of expanding circle maps acting on measures. Ergod. Th. & Dynam. Sys. 33(2) (2013), 529–548.CrossRefGoogle Scholar
Ledrappier, F. and Walters, P.. A relativised variational principle for continuous transformations. J. Lond. Math. Soc. 16(3) (1977), 568–576.CrossRefGoogle Scholar
Lindenstrauss, E. and Tsukamoto, M.. Double variational principle for mean dimension. Geom. Funct. Anal. 29 (2019), 1048–1109.CrossRefGoogle Scholar
Lindenstrauss, E. and Weiss, B.. Mean topological dimension. Israel J. Math. 115 (2000), 1–24.CrossRefGoogle Scholar
Pesin, Y.. Dimension Theory in Dynamical Systems: Contemporary Views and Applications (Lectures in Mathematics). University of Chicago Press, Chicago, 1997.CrossRefGoogle Scholar
Rodrigues, F. and Varandas, P.. Specification properties and thermodynamical properties of semigroup actions. J. Math. Phys. 57 (2016), 052704.10.1063/1.4950928CrossRefGoogle Scholar
Ruelle, D.. On a compact with ${\mathbb{Z}}^p$ -action satisfying expansiveness and specification. Trans. Amer. Math. Soc. 185 (1973), 237–251.CrossRefGoogle Scholar
Tsukamoto, M.. Mean dimension of full shifts. Israel J. Math. 230(1) (2019), 183–193.10.1007/s11856-018-1813-yCrossRefGoogle Scholar
Tsukamoto, M.. Double variational principle for mean dimension with potential. Adv. Math. 361 (2020), 106935, 53 pp.CrossRefGoogle Scholar
Velozo, A. and Velozo, R.. Rate distortion theory, metric mean dimension and measure theoretic entropy. Preprint, 2017, arXiv:1707.05762.Google Scholar