Hostname: page-component-7dd5485656-hw7sx Total loading time: 0 Render date: 2025-10-31T01:40:57.940Z Has data issue: false hasContentIssue false
  • English
  • Français

Weak convergence to extremal processes and record events for non-uniformly hyperbolic dynamical systems

Published online by Cambridge University Press:  07 September 2017

MARK HOLLAND  and
MIKE TODD
MARK HOLLAND
Affiliation:
Mathematics (CEMPS), Harrison Building (327), North Park Road, Exeter EX4 4QF, UK email M.P.Holland@exeter.ac.uk
MIKE TODD
Affiliation:
Mathematical Institute, University of St Andrews, North Haugh, St Andrews KY16 9SS, Scotland, UK email m.todd@st-andrews.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

For a measure-preserving dynamical system 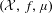$({\mathcal{X}},f,\unicode[STIX]{x1D707})$, we consider the time series of maxima 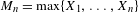$M_{n}=\max \{X_{1},\ldots ,X_{n}\}$ associated to the process 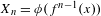$X_{n}=\unicode[STIX]{x1D719}(f^{n-1}(x))$ generated by the dynamical system for some observable 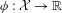$\unicode[STIX]{x1D719}:{\mathcal{X}}\rightarrow \mathbb{R}$. Using a point-process approach we establish weak convergence of the process 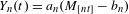$Y_{n}(t)=a_{n}(M_{[nt]}-b_{n})$ to an extremal process 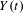$Y(t)$ for suitable scaling constants 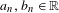$a_{n},b_{n}\in \mathbb{R}$. Convergence here takes place in the Skorokhod space 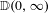$\mathbb{D}(0,\infty )$ with the 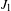$J_{1}$ topology. We also establish distributional results for the record times and record values of the corresponding maxima process.

Information

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 4 , April 2019 , pp. 980 - 1001
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Collet, P.. Statistics of closest return for some non-uniformly hyperbolic systems. Ergod. Th. & Dynam. Sys. 21 (2001), 401–420.Google Scholar
Chazottes, J.-R. and Collet, P.. Poisson approximation for the number of visits to balls in non-uniformly hyperbolic dynamical systems. Ergod. Th. & Dynam. Sys. 33 (2013), 49–80.Google Scholar
Embrechts, P., Klüpperlberg, C. and Mikosch, T.. Modelling extremal events. For Insurance and Finance (Applications of Mathematics, 30) . Springer, Berlin, 1997.Google Scholar
Freitas, A. C. M. and Freitas, J. M.. On the link between dependence and independence in extreme value theory for dynamical systems. Statist. Probab. Lett. 78 (2008), 1088–1093.Google Scholar
Freitas, J., Freitas, A. and Todd, M.. Hitting times and extreme value theory. Probab. Theory Related Fields 147(3) (2010), 675–710.Google Scholar
Freitas, A. C. M., Freitas, J. M. and Todd, M.. Extreme value laws in dynamical systems for non-smooth observations. J. Stat. Phys. 42(1) (2011), 108–126.Google Scholar
Freitas, A. C. M., Freitas, J. M. and Todd, M.. Extremal index, hitting time statistics and periodicity. Adv. Math. 231(5) (2012), 2626–2665.Google Scholar
Gupta, C., Holland, M. P. and Nicol, M.. Extreme value theory for dispersing billiards, Lozi maps and Lorenz maps. Ergod. Th. & Dynam. Sys. 31(5) (2011), 1363–1390.Google Scholar
Gupta, C.. Extreme-value distributions for some classes of non-uniformly partially hyperbolic dynamical systems. Ergod. Th. & Dynam. Sys. 30 (2010), 757–771.Google Scholar
Holland, M. P., Nicol, M. and Török, A.. Extreme value distributions for non-uniformly expanding dynamical systems. Trans. Amer. Math. Soc. 364 (2012), 661–688.Google Scholar
Holland, M. P., Nicol, M. and Török, A.. Almost sure convergence of maxima for chaotic dynamical systems. Stochastic Process. Appl. 126 (2016), 3145–3170.Google Scholar
Kallenberg, O.. Random Measures. Academic Press, New York, 1986.Google Scholar
Leadbetter, M. R., Lindgren, G. and Rootzén, H.. Extremes and Related Properties of Random Sequences and Processes (Springer Series in Statistics) . Springer, New York, 1980.Google Scholar
Resnick, S. I.. Inverses of extremal processes. Adv. Appl. Probab. 6 (1973), 392–406.Google Scholar
Resnick, S. I.. Weak convergence to extremal processes. Ann. Probab. 3(6) (1975), 951–960.Google Scholar
Resnick, S. I.. Extreme values, regular variation, and point processes. Applied Probability (Applied Probability Trust Series, 4) . Springer, New York, 1987.Google Scholar
Skorokhod, A. V.. Limit theorems for stochastic processes. Theory Probab. Appl. 1 (1957), 261–290.Google Scholar
Tyran-Kamińska, M.. Weak convergence to Lévy stable processes in dynamical systems. Stoch. Dyn. 10 (2010), 263–289.Google Scholar
Young, L.-S.. Recurrence times and rates of mixing. Israel J. Math. 110 (1999), 153–188.Google Scholar
Zhang, L.. Borel Cantelli lemmas and extreme value theory for geometric Lorenz models. Nonlinearity 29(1) (2015), 232–256.Google Scholar