Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-10T19:35:56.330Z Has data issue: false hasContentIssue false
  • English
  • Français

Null controllability of the heat equationin unbounded domainsby a finite measure control region

Published online by Cambridge University Press:  15 June 2004

Piermarco Cannarsa ,
Patrick Martinez  and
Judith Vancostenoble
Piermarco Cannarsa
Affiliation:
Dipartimento di Matematica, Università di Roma “Tor Vergata”, Via della Ricerca Scientifica, 00133 Roma, Italy; cannarsa@mat.uniroma2.it.
Patrick Martinez
Affiliation:
Laboratoire M.I.P., UMR CNRS 5640, Université Paul Sabatier Toulouse III, 118 route de Narbonne, 31062 Toulouse Cedex 4, France; martinez@mip.ups-tlse.fr.; cancoste@mip.ups.tlse.fr.
Judith Vancostenoble
Affiliation:
Laboratoire M.I.P., UMR CNRS 5640, Université Paul Sabatier Toulouse III, 118 route de Narbonne, 31062 Toulouse Cedex 4, France; martinez@mip.ups-tlse.fr.; cancoste@mip.ups.tlse.fr.
Get access

Abstract

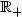Motivated by two recent works of Micu and Zuazua and Cabanillas, De Menezes and Zuazua, we study the null controllability of the heat equationin unbounded domains, typically $\mathbb R_+$ or  $\mathbb R^N$ 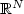. Considering an unbounded and disconnected control region of the form $\omega := \cup _n \omega _n$ 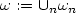, we prove two null controllability results:under some technical assumption on the control parts $\omega _n$ , we provethat every initial datum in some weighted L 2 space can be controlled to zero by usual control functions, and every initial datum in L 2(Ω) can be controlled to zero usingcontrol functions in a weighted L 2 space.At last we give several examples in which the control region has a finite measure and our null controllability results apply.

Keywords

Null controllabilityweighted observability inequalities.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 10 , Issue 3 , July 2004 , pp. 381 - 408
Copyright
© EDP Sciences, SMAI, 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

P. Albano and P. Cannarsa, Lectures on Carleman estimates for elliptic and parabolic operators with applications (in preparation).
Aniţa, S. and Barbu, V., Null controllability of nonlinear convective heat equations. ESAIM: COCV 5 (2000) 157-173. CrossRef
V.R. Cabanillas, S.B. De Menezes and E. Zuazua, Null controllability in unbounded domains for the semilinear heat equation with nonlinearities involving gradient terms. J. Optim. Theory Appl. 110 (2001) 245-264.
Cannarsa, P., Martinez, P. and Vancostenoble, J., Nulle contrôlabilité régionale pour des équations de la chaleur dégénérées. Comptes Rendus Mécanique 330 (2002) 397-401. CrossRef
De Teresa, L., Approximate controllability of a semilinear heat equation in $\mathbb R ^n$ . SIAM J. Control Optim. 36 (1998) 2128-2147. CrossRef
L. De Teresa and E. Zuazua, Approximate controllability of the semilinear heat equation in unbounded domains. Nonlinear Anal. TMA 37 (1999) 1059-1090.
Sz. Dolecki, D.L. Russell, A general theory of observation and control. SIAM J. Control Optim. 15 (1977) 185-220. CrossRef
Fabre, C., Puel, J.P. and Zuazua, E., Approximate controllability of the semilinear heat equation. Proc. Roy. Soc. Edinb. A 125 (1995) 185-220. CrossRef
H.O. Fattorini and D.L. Russell, Exact controllability theorems for linear parabolic equations in one space dimension. Arch. Rat. Mech. Anal. 4 (1971) 272-292.
Fattorini, H.O. and Russell, D.L., Uniform bounds on biorthogonal functions for real exponentials with an application to the control theory of parabolic equations. Quart. Appl. Math. 32 (1974) 45-69. CrossRef
Fernández-Cara, E., Null controllability of the semilinear heat equation. ESAIM: COCV 2 (1997) 87-103. CrossRef
Fernández-Cara, E. and Zuazua, E., The cost of approximate controllability for heat equations: the linear case. Adv. Differ. Equations 5 (2000) 465-514.
Fernández-Cara, E. and Zuazua, E., Controllability for weakly blowing-up semilinear heat equations. Ann. Inst. H. Poincaré Anal. Non Linéaire 17 (2000) 583-616. CrossRef
A.V. Fursikov and O. Yu Imanuvilov, Controllability of evolution equations, Seoul National University, Seoul, Korea. Lect. Notes Ser. 34 (1996).
Imanuvilov, O. Yu., Boundary controllability of parabolic equations. Russian Acad. Sci. Sb. Math. 186 (1995) 109-132.
Jones Jr, B.F.., A fundamental solution for the heat equation which is supported in a strip. J. Math. Anal. Appl. 60 (1977) 314-324. CrossRef
Khapalov, A., Mobile points controls versus locally distributed ones for the controllability of the semilinear parabolic equations. SIAM J. Control Optim. 40 (2001) 231-252. CrossRef
I. Lasiecka and R. Triggiani, Carleman estimates and exact boundary controllability for a system of coupled, non conservative second order hyperbolic equations, in Partial Differential Equations Methods in Control and Shape Analysis. Marcel Dekker, New York, Lect. Notes Pure Appl. Math. 188 (1994) 215-243.
Lebeau, G. and Robbiano, L., Contrôle exact de l'équation de la chaleur. Comm. Partial Differ. Equations 20 (1995) 335-356. CrossRef
Micu, S. and Zuazua, E., On the lack of null controllability of the heat equation on the half-line. Trans. Amer. Math. Soc. 353 (2001) 1635-1659. CrossRef
S. Micu and E. Zuazua, On the lack of null controllability of the heat equation on the half-space. Portugaliae Math. 58 (2001) 1-24.
Rosier, L., Exact boundary controllability for the linear Korteweg-de Vries equation on the half-line. SIAM J. Control Optim. 39 (2000) 331-351. CrossRef
Russell, D.L., A unified boundary controllability theory for hyperbolic and parabolic partial differential equations. Stud. Appl. Math. 52 (1973) 189-221. CrossRef
Tataru, D., A priori estimates of Carleman's type in domains with boundary. J. Math. Pures Appl. 73 (1994) 355-387.
D. Tataru, Carleman estimates and unique continuation near the boundary for P.D.E.'s. J. Math. Pures Appl. 75 367-408 ((1996).
Zhang, X., A remark on null controllability of the heat equation. SIAM J. Control Optim. 40 (2001) 39-53. CrossRef
Zuazua, E., Approximate controllability for the semilinear heat equation with globally Lipschitz nonlinearities. Control Cybern. 28 (1999) 665-683.