Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T05:10:22.009Z Has data issue: false hasContentIssue false
  • English
  • Français

Resonance of minimizers for n-level quantum systemswith an arbitrary cost

Published online by Cambridge University Press:  15 October 2004

Ugo Boscain  and
Grégoire Charlot
Ugo Boscain
Affiliation:
SISSA-ISAS, via Beirut 2-4, 34014 Trieste, Italy; boscain@sissa.it.;charlot@sissa.it Département de Mathématiques, Analyse Appliquée et Optimisation, Université de Bourgogne, 9 avenue Alain Savary, BP 47870-21078 Dijon Cedex, France.
Grégoire Charlot
Affiliation:
SISSA-ISAS, via Beirut 2-4, 34014 Trieste, Italy; boscain@sissa.it.;charlot@sissa.it
Get access

Abstract

We consider an optimal control problem describing a laser-inducedpopulation transfer on a n-level quantum system. For a convex cost depending only on the moduliof controls (i.e. the lasers intensities),we prove that there always exists a minimizer inresonance. This permits to justifysome strategies used in experimental physics. 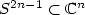It is also quite importantbecause it permits to reduce remarkablythe complexity of the problem (and extend some of our previous resultsfor n=2 and n=3): instead of looking for minimizers on thesphere $S^{2n-1}\subset\mathbb{C}^n$ one is reduced to look just forminimizers on the sphere $S^{n-1}\subset \mathbb{R}^n$ 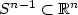. Moreover, for the reduced problem, we investigate on the question of existence of strict abnormal minimizer.

Keywords

Control of quantum systemsoptimal controlsub-Riemannian geometryresonancepontryagin maximum principleabnormal extremalsrotating wave approximation.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 10 , Issue 4 , October 2004 , pp. 593 - 614
Copyright
© EDP Sciences, SMAI, 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

A.A. Agrachev and Yu.L. Sachkov, Control Theory from the Geometric Viewpoint. Springer-Verlag, EMS (2004) 1-410.
Agrachev, A.A. and Sarychev, A.V., Sub-Riemannian metrics: minimality of abnormal geodesics versus subanaliticity. ESAIM: COCV 2 (1997) 377-448. CrossRef
Altafini, C., Controllability of quantum mechanical systems by root space decomposition of $su(N)$ . J. Math. Phys. 43 (2002) 2051-2062. CrossRef
El Assoudi, R., Gauthier, J.P. and Kupka, I.A.K., On subsemigroups of semisimple Lie groups. Ann. Inst. H. Poincaré Anal. Non Linéaire 13 (1996) 117-133. CrossRef
Bellaiche, A., The tangent space in sub-Riemannian geometry. Sub-Riemannian geometry. Progr. Math. 144 (1996) 1-78.
K. Bergmann, H. Theuer and B.W. Shore, Coerent population transfer among quantum states of atomes and molecules. Rev. Mod. Phys. 70 (1998) 1003-1025.
Boltyanskii, V.G., Sufficient Conditions for Optimality and the Justification of the Dynamics Programming Principle. SIAM J. Control Optim. 4 (1996) 326-361. CrossRef
B. Bonnard and M. Chyba, The Role of Singular Trajectories in Control Theory. Springer, SMAI, Vol. 40 (2003).
U. Boscain and B Piccoli, Optimal Synthesis for Control Systems on 2-D Manifolds. Springer, SMAI, Vol. 43 (2004).
Boscain, U., Charlot, G., Gauthier, J.-P., Guérin, S. and Jauslin, H.-R., Optimal Control in laser-induced population transfer for two- and three-level quantum systems. J. Math. Phys. 43 (2002) 2107-2132. CrossRef
Boscain, U., Chambrion, T. and Gauthier, J.-P., On the K+P problem for a three-level quantum system: Optimality implies resonance. J. Dyn. Control Syst. 8 (2002) 547-572. CrossRef
U. Boscain, T. Chambrion and J.-P. Gauthier, Optimal Control on a n-level Quantum System, in Proc. of the 2nd IFAC Workshop on Lagrangian and Hamiltonian Methods for Nonlinear Control, Astolfi, Gordillo and van der Schaft Eds., Elsevier (2003).
W.M. Boothby and E.N. Wilson, Determination of the transitivity of bilinear systems. SIAM J. Control Optim. 17 (1979) 212-221.
Brunovsky, P., Existence of Regular Syntheses for General Problems. J. Differ. Equations 38 (1980) 317-343. CrossRef
Brunovsky, P., Every Normal Linear System Has a Regular Time-Optimal Synthesis. Math. Slovaca 28 (1978) 81-100.
D'Alessandro, D. and Dahleh, M., Optimal control of two-level quantum systems. IEEE Trans. Automat. Control 46 (2001) 866-876. CrossRef
U. Gaubatz, P. Rudecki, M. Becker, S. Schiemann, M. Kulz and K. Bergmann, Population switching between vibrational levels in molecular beams. Chem. Phys. Lett. 149 (1988) 463.
Gauthier, J.P. and Bornard, G., Controlabilite des sytemes bilineaires. SIAM J. Control Optim. 20 (1982) 377-384. CrossRef
Gromov, M., Carnot-Carathéodory spaces seen from within. Sub-Riemannian geometry. Progr. Math. 144 (1996) 79-323.
Hulet, R.G. and Kleppner, D., Rydberg Atoms in “Circular” states. Phys. Rev. Lett. 51 (1983) 1430-1433. CrossRef
V. Jurdjevic, Geometric Control Theory. Cambridge University Press (1997).
Jurdjevic, V. and Kupka, I.K., Control Systems on Semisimple Lie Groups and Their Homogeneous Spaces. Ann. Inst. Fourier 31 (1981) 151-179. CrossRef
V. Jurdjevic and H.J. Sussmann, Controllability of Non-Linear systems. J. Differ. Equation 12 95-116.
N. Khaneja, R. Brockett and S.J. Glaser, Time optimal control in spin systems. Phys. Rev. A 63 (2001).
Khaneja, N. and Glaser, S.J., Cartan decomposition of SU(n) and Control of Spin Systems. J. Chem. Phys. 267 (2001) 11-23.
Liedenbaum, C., Stolte, S. and Reuss, J., Inversion produced and reversed by adiabatic passage. Phys. Rep. 178 (1989) 1-24. CrossRef
R. Montgomery, A Tour of Subriemannian Geometry. American Mathematical Society, Mathematical Surveys and Monographs (2002).
Montgomery, R., A survey of singular curves in sub-Riemannian geometry. J. Dyn. Control Syst. 1 (1995) 49-90. CrossRef
Piccoli, B., Classifications of Generic Singularities for the Planar Time-Optimal Synthesis. SIAM J. Control Optim. 34 (1996) 1914-1946. CrossRef
B. Piccoli and H.J. Sussmann, Regular Synthesis and Sufficiency Conditions for Optimality. SIAM. J. Control Optim. 39 (2000) 359-410.
L.S. Pontryagin, V. Boltianski, R. Gamkrelidze and E. Mitchtchenko, The Mathematical Theory of Optimal Processes. John Wiley and Sons, Inc (1961).
M.A. Daleh, A.M. Peirce and H. Rabitz, Optimal control of quantum-mechanical systems: Existence, numerical approximation, and applications. Phys. Rev. A 37 (1988).
V. Ramakrishna, K.L. Flores, H. Rabitz and R.Ober, Quantum control by decomposition of su(2). Phys. Rev. A 62 (2000).
Sachkov, Y., Controllability of Invariant Systems on Lie Groups and Homogeneous Spaces. J. Math. Sci. 100 (2000) 2355-2427. CrossRef
B.W. Shore, The theory of coherent atomic excitation. New York, NY, Wiley (1990).
Sussmann, H.J., The Structure of Time-Optimal Trajectories for Single-Input Systems in the Plane: the $C^{\infty}$ Nonsingular Case. SIAM J. Control Optim. 25 (1987) 433-465. CrossRef