Asymmetric heteroclinicdouble layers

Abstract

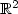Let W be a non-negative function of class C³ from $\xR^2$ to $\xR$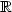, which vanishes exactly at two points a and b. Let S¹(a, b) be the set of functions of a real variable which tend to a at -∞ and to b at +∞ and whose one dimensional energy $$ E_1(v)=\int_\xR\bigl[W(v)+\lvert v'\rvert^2/2\bigr]\,\xdif x $$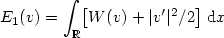 is finite. Assume that there exist two isolated minimizers z₊ and z_- of the energy E₁ over S¹(a, b). Under a mild coercivity condition on the potential W and a generic spectral condition on the linearization of the one-dimensional Euler–Lagrange operator at z₊ and z_-, it is possible to prove that there exists a function u from $\xR^2$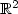 to itself which satisfies the equation $$ -\Delta u + \xDif W(u)^\mathsf{T}=0, $$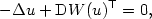 and the boundary conditions $$ \lim_{x_2\to +\infty} u(x_1,x_2)=z_+(x_1-m_+),\phantom{\mathbf{a}} \lim_{x_2\to -\infty} u(x_1,x_2)=z_-(x_1-m_-), \lim_{x_1\to -\infty}u(x_1,x_2)=\mathbf{a},\phantom{z_+(x_1-m_+)} \lim_{x_1\to+\infty}u(x_1,x_2)=\mathbf{b}. 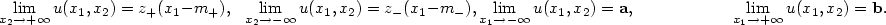$$ The above convergences are exponentially fast; the numbers m₊ and m_- are unknowns of the problem.