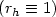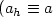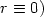Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Paronetto, Fabio
2010.
G-convergence of mixed type evolution operators.
Journal de Mathématiques Pures et Appliquées,
Vol. 93,
Issue. 4,
p.
361.