Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T01:19:51.365Z Has data issue: false hasContentIssue false
  • English
  • Français

Estimate of the pressure when its gradientis the divergence of a measure. Applications

Published online by Cambridge University Press:  28 October 2010

Marc Briane  and
Juan Casado-Díaz
Marc Briane
Affiliation:
Institut de Recherche Mathématique de Rennes, INSA de Rennes, France. mbriane@insa-rennes.fr
Juan Casado-Díaz
Affiliation:
Dpto. de Ecuaciones Diferenciales y Análisis Numérico, Universidad de Sevilla, Spain. jcasadod@us.es
Get access

Abstract

In this paper, a $W^{-1,N'}$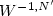 estimate of the pressure is derived when its gradient is the divergence of a matrix-valued measure on $\mathbb R^N$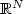, or on a regular bounded open set of $\mathbb R^N$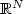. The proof is based partially on the Strauss inequality [Strauss, Partial Differential Equations: Proc. Symp. Pure Math. 23 (1973) 207–214] in dimension two, and on a recent result of Bourgain and Brezis [J. Eur. Math. Soc. 9 (2007) 277–315] in higher dimension. The estimate is used to derive a representation result for divergence free distributions which read as the divergence of a measure, and to prove an existence result for the stationary Navier-Stokes equation when the viscosity tensor is only in L1.

Keywords

PressureNavier-Stokes equationdiv-curlmeasure datafundamental solution
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 17 , Issue 4 , October 2011 , pp. 1066 - 1087
Copyright
© EDP Sciences, SMAI, 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amrouche, C. and Girault, V., Decomposition of vector spaces and application to the Stokes problem in arbitrary dimension. Czechoslovak Math. J. 44 (1994) 109–140.
Bellieud, M. and Bouchitté, G., Homogenization of elliptic problems in a fiber reinforced structure. Nonlocal effects. Ann. Scuola Norm. Sup. Pisa Cl. Sci. 26 (1998) 407–436.
Bogovski, M.E., Solution of the first boundary value problem for the equation of continuity of an incompressible medium. Soviet Math. Dokl. 20 (1979) 1094–1098.
Bourgain, J. and Brezis, H., New estimates for elliptic equations and Hodge type systems. J. Eur. Math. Soc. 9 (2007) 277–315. CrossRef
H. Brezis, Analyse Fonctionnelle, Théorie et Applications. Mathématiques Appliquées pour la Maîtrise, Masson, Paris (1983).
Brezis, H. and Van Schaftingen, J., Boundary estimates for elliptic systems with L 1-data. Calc. Var. 30 (2007) 369–388. CrossRef
Briane, M., Homogenization of the Stokes equations with high-contrast viscosity. J. Math. Pures Appl. 82 (2003) 843–876. CrossRef
Briane, M. and Casado Díaz, J., Compactness of sequences of two-dimensional energies with a zero-order term. Application to three-dimensional nonlocal effects. Calc. Var. 33 (2008) 463–492. CrossRef
Camar-Eddine, M. and Seppecher, P., Determination of the closure of the set of elasticity functionals. Arch. Rat. Mech. Anal. 170 (2003) 211–245. CrossRef
G. de Rham, Variétés différentiables, Formes, courants, formes harmoniques. Hermann, Paris (1973).
D. Gilbarg and N. Trudinger, Elliptic Partial Differential Equations of Second Order. Springer, Berlin (2001).
Hopf, E., Über die Anfwangswertaufgabe für die hydrodynamischen Grundgleichungen. Math. Nachr. 4 (1951) 213–231. CrossRef
E.Y. Khruslov, Homogenized models of composite media, in Composite Media and Homogenization Theory, G. Dal Maso and G.F. Dell'Antonio Eds., Progress in Nonlinear Differential Equations and Their Applications, Birkhäuser (1991) 159–182.
O.A. Ladyzhenskaya, The mathematical theory of viscous incompressible flow, Mathematics and its Applications 2. Gordon and Breach, Science Publishers, New York-London-Paris (1969).
Lions, J.-L., Quelques résultats d'existence dans des équations aux dérivées partielles non linéaires. Bull. S.M.F. 87 (1959) 245–273.
V.A. Marchenko and E.Y. Khruslov, Homogenization of partial differential equations, Progress in Mathematical Physics 46. Birkhäuser, Boston (2006).
J. Nečas, Équations aux dérivées partielles. Presses de l'Université de Montréal (1965).
Pideri, C. and Seppecher, P., A second gradient material resulting from the homogenization of an heterogeneous linear elastic medium. Continuum Mech. Thermodyn. 9 (1997) 241–257. CrossRef
M.-J. Strauss, Variations of Korn's and Sobolev's inequalities, in Partial Differential Equations: Proc. Symp. Pure Math. 23, D. Spencer Ed., Am. Math. Soc., Providence (1973) 207–214.
Tartar, L., Topics in nonlinear analysis. Publications Mathématiques d'Orsay 78 (1978) 271.
R. Temam, Navier-Stokes Equations – Theory and Numerical Analysis, Studies in Mathematics and its Applications 2. North-Holland, Amsterdam (1984).
Van Schaftingen, J., Estimates for L 1-vector fields under higher-order differential conditions. J. Eur. Math. Soc. 10 (2008) 867–882. CrossRef
J. Van Schaftingen, Estimates for L 1-vector fields. C. R. Acad. Sci. Paris, Ser. I 339 (2004) 181–186.