Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-10T21:34:25.218Z Has data issue: false hasContentIssue false
  • English
  • Français

Hamilton-Jacobi equations for control problemsof parabolic equations

Published online by Cambridge University Press:  22 March 2006

Sophie Gombao  and
Jean-Pierre Raymond
Sophie Gombao
Affiliation:
Laboratoire MIP, UMR CNRS 5640, Université Paul Sabatier, 31062 Toulouse Cedex 4, France; gombao@cict.fr; raymond@mip.ups-tlse.fr
Jean-Pierre Raymond
Affiliation:
Laboratoire MIP, UMR CNRS 5640, Université Paul Sabatier, 31062 Toulouse Cedex 4, France; gombao@cict.fr; raymond@mip.ups-tlse.fr
Get access

Abstract

We study Hamilton-Jacobi equations related to the boundary (or internal) control of semilinear parabolic equations, including the case of a control acting in a nonlinear boundary condition, or the case of a nonlinearity of Burgers' type in 2D. To deal with a control acting in a boundary condition a fractional power $(-A)^\beta$ 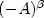– where (A,D(A)) is an unbounded operator in a Hilbert space X – is contained in the Hamiltonian functional appearing in the Hamilton-Jacobi equation. This situation has already been studied in the literature. But, due to the nonlinear term in the state equation, the same fractional power $(-A)^\beta$ 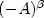appears in another nonlinear term whose behavior is different from the one of the Hamiltonian functional. We also consider cost functionals which are not bounded in bounded subsets in X, but only in bounded subsets in a space $Y\hookrightarrow X$ 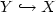. To treat these new difficulties, we show that the value function of control problems we consider is equal in bounded sets in Y to the unique viscosity solution of some Hamilton-Jacobi-Bellman equation. We look for viscosity solutions in classes of functions which are Hölder continuous with respect to the time variable.

Keywords

Hamilton-Jacobi-Bellman equationboundary controlsemilinear parabolic equations.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 12 , Issue 2 , April 2006 , pp. 311 - 349
Copyright
© EDP Sciences, SMAI, 2006

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

H. Amann, Linear and quasilinear parabolic problems. Vol. I, Abstract linear theory. Birkhäuser Boston Inc., Boston, MA. Monographs Math. 89 (1995).
V. Barbu and G. Da Prato, Hamilton-Jacobi equations in Hilbert spaces, Pitman (Advanced Publishing Program), Boston, MA Res. Notes Math. 86 (1983).
A. Bensoussan, G. Da Prato, M.C. Delfour and S.K. Mitter, Representation and control of infinite-dimensional systems. Vol. 1. Systems & Control: Foundations & Applications. Birkhäuser Boston Inc., Boston, MA (1992).
A. Bensoussan, G. Da Prato, M.C. Delfour and S.K. Mitter, Representation and control of infinite-dimensional systems. Vol. 2. Systems & Control: Foundations & Applications. Birkhäuser Boston Inc., Boston, MA (1993).
Cannarsa, P. and Frankowska, H., Value function and optimality condition for semilinear control problems. II. Parabolic case. Appl. Math. Optim. 33 (1996) 1–33. CrossRef
P. Cannarsa and M.E. Tessitore, Cauchy problem for the dynamic programming equation of boundary control. Boundary control and variation (1994) 13–26.
Cannarsa, P. and Tessitore, M.E., Cauchy problem for Hamilton-Jacobi equations and Dirichlet boundary control problems of parabolic type, in Control of partial differential equations and applications (Laredo, 1994), Dekker, New York. Lect. Notes Pure Appl. Math. 174 (1996) 31–42.
Cannarsa, P. and Tessitore, M.E., Dynamic programming equation for a class of nonlinear boundary control problems of parabolic type. Cont. Cybernetics 25 (1996) 483–495. Distributed parameter systems: modelling and control (1995).
Cannarsa, P. and Tessitore, M.E., Infinite-dimensional Hamilton-Jacobi equations and Dirichlet boundary control problems of parabolic type. SIAM J. Control Optim. 34 (1996) 1831–1847. CrossRef
Crandall, M.G. and Lions, P.-L., Hamilton-Jacobi equations in infinite dimensions. I. Uniqueness of viscosity solutions. J. Funct. Anal. 62 (1985) 379–396. CrossRef
Crandall, M.G. and Lions, P.-L., Hamilton-Jacobi equations in infinite dimensions. II. Existence of viscosity solutions. J. Funct. Anal. 65 (1986) 368–405. CrossRef
Crandall, M.G. and Lions, P.-L., Hamilton-Jacobi equations in infinite dimensions. III. J. Funct. Anal. 68 (1986) 214–247. CrossRef
Crandall, M.G. and Lions, P.-L., Viscosity solutions of Hamilton-Jacobi equations in infinite dimensions. IV. Hamiltonians with unbounded linear terms. J. Funct. Anal. 90 (1990) 237–283. CrossRef
Crandall, M.G. and Lions, P.-L., Viscosity solutions of Hamilton-Jacobi equations in infinite dimensions. V. Unbounded linear terms and B-continuous solutions. J. Funct. Anal. 97 (1991) 417–465. CrossRef
Crandall, M.G. and Lions, P.-L., Hamilton-Jacobi equations in infinite dimensions. VI. Nonlinear A and Tataru's method refined, in Evolution equations, control theory, and biomathematics (Han sur Lesse 1991), Dekker, New York. Lect. Notes Pure Appl. Math. 155 (1994) 51–89.
Crandall, M.G. and Lions, P.-L., Viscosity solutions of Hamilton-Jacobi equations in infinite dimensions. VII. The HJB equation is not always satisfied. J. Funct. Anal. 125 (1994) 111–148. CrossRef
S Gombao, Équations de Hamilton-Jacobi-Bellman pour des problèmes de contrôle d'équations paraboliques semi-linéaires. Approche théorique et numérique. Université Paul Sabatier, Toulouse (2004).
Gozzi, F., Sritharan, S.S. and A. Święch, Viscosity solutions of dynamic-programming equations for the optimal control of the two-dimensional Navier-Stokes equations. Arch. Ration. Mech. Anal. 163 (2002) 295–327. CrossRef
D. Henry, Geometric theory of semilinear parabolic equations, Springer-Verlag, Berlin. Lect. Notes Math. 840 (1981).
Ishii, H., Viscosity solutions for a class of Hamilton-Jacobi equations in Hilbert spaces. J. Funct. Anal. 105 (1992) 301–341. CrossRef
J.-L. Lions and E. Magenes, Problèmes aux limites non homogènes et applications. Vol. 1. Travaux et Recherches Mathématiques, No. 17. Dunod, Paris (1968).
Rankin, S.M., Semilinear, III. evolution equations in Banach spaces with application to parabolic partial differential equations. Trans. Amer. Math. Soc. 336 (1993) 523–535. CrossRef
Raymond, J.-P., Nonlinear boundary control of semilinear parabolic problems with pointwise state constraints. Discrete Contin. Dynam. Syst. 3 (1997) 341–370. CrossRef
Raymond, J.-P. and Zidani, H., Hamiltonian Pontryagin's principles for control problems governed by semilinear parabolic equations. Appl. Math. Optim. 39 (1999) 143–177. CrossRef
T. Runst and W. Sickel, Sobolev spaces of fractional order, Nemytskij operators, and nonlinear partial differential equations, Walter de Gruyter & Co., Berlin, de Gruyter Series in Nonlinear Analysis and Applications 3 (1996).
Shimano, K., A class of Hamilton-Jacobi equations with unbounded coefficients in Hilbert spaces. Appl. Math. Optim. 45 (2002) 75–98. CrossRef
Soner, H.M., On the Hamilton-Jacobi-Bellman equations in Banach spaces. J. Optim. Theory Appl. 57 (1988) 429–437. CrossRef
Tataru, D., Viscosity solutions for the dynamic programming equations. Appl. Math. Optim. 25 (1992) 109–126. CrossRef
Tataru, D., Viscosity solutions for Hamilton-Jacobi equations with unbounded nonlinear term: a simplified approach. J. Differ. Equ. 111 (1994) 123–146. CrossRef