Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-28T12:55:17.630Z Has data issue: false hasContentIssue false
  • English
  • Français

Limitations on the control of Schrödinger equations

Published online by Cambridge University Press:  11 October 2006

Reinhard Illner ,
Horst Lange  and
Holger Teismann
Reinhard Illner
Affiliation:
Department of Mathematics and Statistics, University of Victoria, PO Box 3045, Victoria, B.C., V8W 3P4 Canada; rillner@math.uvic.ca
Horst Lange
Affiliation:
Mathematisches Institut, Universität Köln, Weyertal 86-90, 50931 Köln, Germany; lange@mathematik.uni-koeln.de
Holger Teismann
Affiliation:
Department of Mathematics and Statistics, Acadia University, Wolfville, N.S., B4P 1R6 Canada; hteisman@acadiau.ca
Get access

Abstract

We give the definitions of exact and approximate controllability forlinear and nonlinear Schrödinger equations, review fundamental criteria for controllability and revisit a classical “No-go” resultfor evolution equations due to Ball, Marsden and Slemrod. 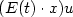In Section 2 we prove corresponding results on non-controllabilityfor the linear Schrödinger equation and distributed additive control,and we show that the Hartree equation of quantum chemistry with bilinearcontrol $(E(t)\cdot x) u$ is not controllable in finite or infinite time. Finally, in Section 3, we give criteria for additive controllability of linear Schrödinger equations, andwe give a distributed additive controllability result for the nonlinear Schrödinger equation if the data are small.

Keywords

Schrödinger equationsexact and approximate controlquantum control.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 12 , Issue 4 , October 2006 , pp. 615 - 635
Copyright
© EDP Sciences, SMAI, 2006

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdullaev, F.Kh. and Garnier, J., Collective oscillations of one-dimensional Bose-Einstein gas under varying in time trap potential and atomic scattering length. Phys. Rev. A 70 (2004) 053604. CrossRef
G. Bachman and N. Narici, Functional Analysis. Academic Press, N.Y. (1966).
Ball, J., Marsden, J. and Slemrod, M., Controllability for distributed bilinear systems. SIAM J. Contr. Opt. 20 (1982) 575-597. CrossRef
Bardos, C., Lebeau, G. and Rauch, J., Sharp sufficient conditions for the observation, control, and stabilization of waves from the boundary. SIAM J. Contr. Opt. 30 (1992) 1024-1065. CrossRef
L. Baudouin, A bilinear optimal control problem applied to a time dependent Hartree-Fock equation coupled with classical nuclear dynamics. Portugaliae Mat. (To appear).
Baudouin, L., Existence and regularity of the solution of a time dependent Hartree-Fock equation coupled with a classical nuclear dynamics. Rev. Mat. Complut. 18 (2005) 285-314. CrossRef
L. Baudouin and J.-P. Puel, Bilinear optimal control problem on a Schrödinger equation with singular potentials. Preprint (2004).
K. Beauchard, Local controllability of a 1-D Schrödinger equation, J. Math. Pures Appl. 84 (2005) 851-956. CrossRef
Beauchard, K. and Coron, J.M., Controllability of a quantum particle in a moving potential well. J. Funct. Anal. 232 (2006) 328-389. CrossRef
P.W. Brumer and M. Shapiro, Principles of the Quantum Control of Molecular Processes. Wiley-VCH, Berlin (2003).
R. Carles, Linear vs. nonlinear effects for nonlinear Schrödinger equations with potential. Commun. Contemp. Math. 7(4) (2005) 483-508.
Cancès, E. and LeBris, C., On the time-dependent Hartree-Fock equations coupled with classical nuclear dynamics. Math. Mod. Meth. Appl. Sci. 9 (1999) 963-990. CrossRef
E. Cancès, C. LeBris and M. Pilot, Contrôle optimale bilinéaire d'une équation de Schrödinger. C. R. Acad. Sci. Paris, Sér. 1 330 (2000) 567-571.
Clark, J.W., Lucarelli, D.G. and Tarn, T.J., Control of quantum systems. Int. J. Mod. Phys. B 17 (2003) 5397-5412. CrossRef
Fabre, C., Résultats de contrôlabilité exacte interne pour l'équation de Schrödinger at leurs limites asymptotiques, Application à certaines équations de plaques vibrantes. Asymptotic Analysis 5 (1992) 343-379.
H. Helson, Harmonic Analysis. Addison-Wesley, Reading (1983).
Holthaus, M. and Stenholm, S., Coherent control of self-trapping transition. Eur. Phys. J. B 20 (2001) 451-467. CrossRef
Huang, G.M, Tarn T.J and J.W. Clark, On the controllability of quantum-mechanical systems. J. Math. Phys. 24 (1983) 2608-2618. CrossRef
Husimi, H., Miscellanea in elementary quantum mechanics II. Prog. Theor. Phys. 9 (1953) 381-402. CrossRef
Illner, R., Lange, H. and Teismann, H., A note on the exact internal control of nonlinear Schrödinger equations. CRM Proc. Lecture Notes 33 (2003) 127-137. CrossRef
Ingham, A.E., Some trigonometric inequalities with applications to the theory of series. Math. Z. 41 (1936) 367. CrossRef
Journé, J.L., Soffer, A. and Sogge, C.D., Decay estimates for Schrödinger operators. Commun. Pure Appl. Math. 44 (1991) 573-604. CrossRef
Kerner, K.H., Note on the forced and damped oscillator in quantum mechanics. Can. J. Phys. 36 (1958) 371-377. CrossRef
Lan, C., Tarn, T.J., Chi, Q.-S. and Clark, J.W., Analytic controllability of time-dependent quantum control systems. J. Math. Phys. 46 (2005) 052102 CrossRef
Lasiecka, I. and Triggiani, R., Optimal regularity, exact controllability and uniform stabilization of Schrödinger equations with Dirichlet controls. Differ. Int. Equ. 5 (1992) 571-535.
I. Lasiecka and R. Triggiani, Control theory for partial differential equations, continuous and approximation theories. I & II. Cambridge University Press, Cambridge (2000).
Lasiecka, I., Triggiani, R. and Zhang, X., Global uniqueness, observability and stabilization of nonconservative Schrödinger equations via pointwise Carleman estimates. I. $H\sp 1(\Omega)$ -estimates. J. Inverse Ill-Posed Probl. 12 (2004) 43-123.
Lasiecka, I., Triggiani, R. and Zhang, X., Global uniqueness, observability and stabilization of nonconservative Schrödinger equations via pointwise Carleman estimates. II. $L\sb 2(\Omega)$ -estimates. J. Inverse Ill-Posed Probl. 12 (2004) 183-231.
Lebeau, G., Contrôle de l'équation de Schrödinger. Jour. Math. Pures Appl. 71 (1992) 267-291.
C. LeBris, Control theory applied to quantum chemistry, some tracks, in Conf. Int. contrôle des systèmes gouvernés par des équations aux derivées partielles. ESAIM Proc. 8 (2000) 77-94.
C. LeBris, Computational Chemistry, in Handbook of Numerical Analysis, C. LeBris, Ph.G. Ciarlet Eds. North-Holland, Amsterdam (2003).
J.-L. Lions, Contrôlabilité exacte, perturbations et stabilisation de systèmes distribués. Tome 1 & 2. Masson, Paris (1988).
E. Machtyngier, Exact controllability for the Schrödinger equation. SIAM J. Contr. Opt. 32 (1994) 24-34. CrossRef
Machtyngier, E. and Zuazua, E., Stabilization of the Schrödinger equation. Portugaliae Mat. 51 (1994) 243-256.
Mirrahimi, M. and Rouchon, P., Controllability of quantum harmonic oscillators. IEEE Trans. Automatic Control 49 (2004) 745-747. CrossRef
Phung, K.-D., Observability and control of Schrödinger equations. SIAM J. Contr. Opt. 40 (2001) 211-230. CrossRef
S.A. Rice and M. Zhao, Optical Control of Molecular Dynamics. John Wiley & Sons, New York (2000).
D.L. Russell, Controllability and stabilizability theory for linear partial differential equations, recent progress and open questions. SIAM Rev. (1978) 20 639-739.
Schirmer, S.G., Leahy, J.V. and Solomon, A.I., Degrees of controllability for quantum systems and application to atomic systems. J. Phys. A 35 (2002) 4125-4141. CrossRef
Shustov, A.P., Coherent states and energy spectrum of the anharmonic osciallator. J. Phys. A 11 (1978) 1771-1780. CrossRef
E.M. Stein, Singular Integrals and Differentiability Properties of Functions. Princeton University Press (1974).
G. Turinici, Analyse de méthodes numériques de simulation et contrôle en chimie quantique. Ph.D. Thesis, Univ. Paris VI (2000).
G. Turinici, Controllable quantities for bilinear quantum systems, in Proc. of the 39th IEEE Conference on Decision and Control, Sydney, Australia (2000) 1364-1369.
R.M. Young, An Introduction to Nonharmonic Fourier Series. Academic Press, New York (1980).
J. Zabczyk, Introduction to Control Theory. Birkhäuser, Basel (1994).
Zuazua, E., Remarks on the controllability of the Schrödinger equation. CRM Proc. Lecture Notes 33 (2003) 193-211. CrossRef