Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-13T05:10:30.250Z Has data issue: false hasContentIssue false
  • English
  • Français

Model problems from nonlinear elasticity:partial regularity results

Published online by Cambridge University Press:  14 February 2007

Menita Carozza  and
Antonia Passarelli di Napoli
Menita Carozza
Affiliation:
Dipartimento Pe.Me.Is., Piazza Arechi II, 82100 Benevento, Italy; carozza@unisannio.it
Antonia Passarelli di Napoli
Affiliation:
Dipartimento di Matematica e Appl. “R.Caccioppoli” Universitá di Napoli “Federico II” Via Cintia, 80126 Napoli, Italy; antonia.passarelli@unina.it
Get access

Abstract

In this paper we prove that every weakand strong localminimizer $u\in{W^{1,2}(\Omega,\mathbb{R}^3)}$ 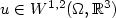of the functional $I(u)=\int_\Omega|Du|^2+f({\rm Adj}Du)+g({\rm det}Du),$ 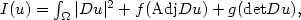where $ u:\Omega\subset\mathbb{R}^3\to \mathbb{R}^3$ 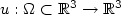, f grows like $|{\rm Adj}Du|^p$ 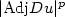, g growslike $|{\rm det}Du|^q$ 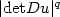and1<q<p<2, is $C^{1,\alpha}$ 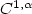on an opensubset $\Omega_0$ 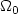of Ω such that ${\it meas}(\Omega\setminus \Omega_0)=0$ 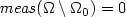. Suchfunctionals naturally arise from nonlinear elasticity problems. The keypoint in order to obtain the partial regularity result is toestablish an energy estimate of Caccioppoli type, which is based onan appropriate choice of the test functions. The limit case $p=q\le 2$ 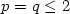is also treated for weak local minimizers.

Keywords

Nonlinearelasticitypartial regularitypolyconvexity.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 13 , Issue 1 , January 2007 , pp. 120 - 134
Copyright
© EDP Sciences, SMAI, 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acerbi, E. and Fusco, N., A regularity theorem for minimizers of quasiconvex integrals. Arch. Rational Mech. Anal. 99 (1987) 261–281. CrossRef
Acerbi, E. and Fusco, N., Regularity for minimizers of non-quadratic functionals: the case $1<p<2$ . J. Math. Anal. Appl. 140 (1989) 115–135. CrossRef
Ball, J.M., Convexity conditions and existence theorems in nonlinear elasticity. Arch. Rational Mech. Anal. 63 (1977) 337–403. CrossRef
J.M. Ball, Some open problem in elasticity, in Geometry, Mechanics and dynamics, Springer, New York (2002) 3–59.
Carozza, M., Fusco, N. and Mingione, G., Partial regularity of minimizers of quasiconvex integrals with subquadratic growth. Annali Mat. Pura Appl. 175 (1998) 141–164. CrossRef
Carozza, M. and Passarelli di, A. Napoli, A regularity theorem for minimizers of quasiconvex integrals the case $1<p<2$ . Proc. Roy. Soc. Edinburgh 126A (1996) 1181–1199. CrossRef
Carozza, M. and Passarelli di, A. Napoli, Partial regularity of local minimizers of quasiconvex integrals with sub-quadratic growth. Proc. Roy. Soc Edinburgh 133A (2003) 1249–1262. CrossRef
B. Dacorogna, Direct methods in the calculus of variations. Appl. Math. Sci. 78, Springer Verlag (1989).
Evans, L.C., Quasiconvexity and partial regularity in the calculus of variations. Arch. Rational Mech. Anal. 95 (1986) 227–252. CrossRef
Fusco, N. and Hutchinson, J., Partial regularity in problems motivated by nonlinear elasticity. SIAM J. Math. 22 (1991) 1516–1551. CrossRef
Fusco, N. and Hutchinson, J., Partial regularity and everywhere continuity for a model problem from nonlinear elasticity. J. Australian Math. Soc. 57 (1994) 149–157. CrossRef
M. Giaquinta, Multiple integrals in the calculus of variations and nonlinear elliptic systems. Ann. Math. Stud. 105 Princeton Univ. Press (1983).
M. Giaquinta and G. Modica, Partial regularity of minimizers of quasiconvex integrals. Ann. Inst. H. Poincaré, Analyse non linéaire 3 (1986) 185–208.
E. Giusti, Metodi diretti in calcolo delle variazioni. U.M.I. (1994).
Kristensen, J. and Taheri, A., Partial regularity of strong local minimizers in the multidimensional calculus of variations. Arch. Rational Mech. Anal. 170 (2003) 63–89. CrossRef
A. Passarelli di Napoli, A regularity result for a class of polyconvex functionals. Ricerche di Matematica XLVIII (1999) 379–393.