Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T12:42:16.788Z Has data issue: false hasContentIssue false
  • English
  • Français

Morse index and bifurcation of p-geodesics on semi Riemannian manifolds

Published online by Cambridge University Press:  26 July 2007

Monica Musso ,
Jacobo Pejsachowicz  and
Alessandro Portaluri
Monica Musso
Affiliation:
Dipartimento di Matematica, Politecnico di Torino, Torino, Italy; jacobo.pejsachowicz@polito.it Departamento de Matematicas, Pontificia Universidad Catolica de Chile, Avenida Vicuña MacKenna 4860, Macul, Chile; mmusso@mat.puc.cl
Jacobo Pejsachowicz
Affiliation:
Dipartimento di Matematica, Politecnico di Torino, Torino, Italy; jacobo.pejsachowicz@polito.it
Alessandro Portaluri
Affiliation:
Departamento de Matemática, Instituto de Matemática e Estatística, Universidade de São Paulo, Rua do Matão 1010, CEP 05508-900, São Paulo, SP Brazil; portalur@ime.usp.br Dipartimento di Matematica, Politecnico di Torino, Italy.
Get access

Abstract

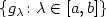Given a one-parameter family $\{g_\lambda\colon\lambda\in [a,b]\}$ of semi Riemannian metrics on ann-dimensional manifold M, a family of time-dependent potentials $\{ V_\lambda\colon \lambda\in [a,b]\}$ 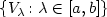and a family $\{\sigma_\lambda\colon \lambda\in [a,b]\} $ 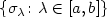of trajectories connecting two points of the mechanical system defined by $(g_\lambda, V_\lambda)$ 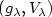, we show that there are trajectories bifurcating from the trivial branch $\sigma_\lambda$ 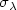if the generalized Morse indices $\mu(\sigma_a)$ 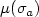and $\mu(\sigma_b)$ 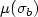are different. If the data are analytic we obtain estimates for the number of bifurcation points on the branch and, in particular, for the number of strictly conjugate points along a trajectory using an explicit computation of the Morse index inthe case of locally symmetric spaces and a comparison principle of Morse Schöenberg type.

Keywords

Generalized Morse indexsemi-Riemannian manifoldsperturbed geodesicbifurcation
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 13 , Issue 3 , July 2007 , pp. 598 - 621
Copyright
© EDP Sciences, SMAI, 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

R. Abraham and J.E. Marsden, Foundations of Mechanics, 2nd edition. Benjamin/Cummings, Ink. Massachusetts (1978).
Andersson, L. and Howard, R., Comparison and rigidity theorems in Semi-Riemannian geometry. Comm. Anal. Geom. 6 (1998) 819–877. CrossRef
Angenent, S.B. and van der Vorst, R., A priori bounds and renormalized Morse indices of solutions of an elliptic system. Ann. Inst. H. Poincaré Anal. Non Linéaire 17 (2000) 277–306. CrossRef
V.I. Arnol'd, Sturm theorems and symplectic geometry. Funktsional. Anal. i Prilozhen. 19 (1985) 1–10.
J.K. Beem, P.E. Ehrlich and K.L. Easley, Global Lorentzian Geometry. Mercel Dekker, Inc. New York and Basel (1996).
Benci, V., Giannoni, F. and Masiello, A., Some properties of the spectral flow in semiriemannian geometry. J. Geom. Phys. 27 (1998) 267–280. CrossRef
A.L. Besse, Manifolds all of whose geodesics are closed. Ergebnisse der Mathematik und ihrer Grenzgebiete 93, Springer-Verlag (1978).
O. Bolza, Lectures on Calculus of Variation. Univ. Chicago Press, Chicago (1904).
Cappell, S.E., Lee, R. and Miller, E.Y., On the Maslov index. Comm. Pure Appl. Math. 47 (1994) 121–186. CrossRef
I. Chavel, Riemannian geometry: a modern introduction, in Cambridge tracts in Mathematics 108, Cambridge Univerisity Press (1993).
Chossat, P., Lewis, D., Ortega, J.P. and Ratiu, T.S., Bifurcation of relative equilibria in mechanical systems with symmetry. Adv. Appl. Math. 31 (2003) 10–45. CrossRef
Conley, C. and Zehnder, E., The Birhoff-Lewis fixed point theorem and a conjecture of V.I. Arnold. Invent. Math. 73 (1983) 33–49. CrossRef
M. Crabb and I. James, Fibrewise Homotopy Theory. Springer-Verlag (1998).
Daniel, M., An extension of a theorem of Nicolaescu on spectral flow and Maslov index. Proc. Amer. Math. Soc. 128 (1999) 611–619. CrossRef
K. Deimling, Nonlinear Functional Analysis. Springer-Verlag (1985).
I. Ekeland, Convexity methods in Hamiltonian systems. Ergebnisse der Mathematik und ihrer Grenzgebiete 19, Springer-Verlag, Berlin (1990).
Guihua Fei, Relative Morse, index and its application to Hamiltonian systems in the presence of symmetries. J. Diff. Eq. 122 (1995) 302–315.
Fitzpatrick, P.M. and Pejsachowicz, J., Parity and generalized multiplicity. Trans. Amer. Math. Soc. 326 (1991) 281–305. CrossRef
Fitzpatrick, P.M., Pejsachowicz, J. and Recht, L., Spectral flow and bifurcation of critical points of strongly-indefinite functional. Part I. General theory. J. Funct. Anal. 162 (1999) 52–95. CrossRef
Fitzpatrick, P.M., Pejsachowicz, J. and Recht, L., Spectral flow and bifurcation of critical points of strongly-indefinite functional. Part II. Bifurcation of periodic orbits of Hamiltonian systems. J. Differ. Eq. 161 (2000) 18–40. CrossRef
Floer, A., Relative Morse index for the symplectic action. Comm. Pure Appl. Math. 41 (1989) 335–356. CrossRef
I.M. Gel'fand and S.V. Fomin, Calculus of Variations. Prentic-Hall Inc., Englewood Cliffs, New Jersey, USA (1963).
I.M. Gel'fand and V.B. Lidskii, On the structure of the regions of stability of linear canonical systems of differential equations with periodic coefficients. Amer. Math. Soc. Transl. Ser. 2 8 (1958) 143–181.
R. Giambó, P. Piccione and A. Portaluri, On the Maslov Index of Lagrangian paths that are not transversal to the Maslov cycle. Semi-Riemannian index Theorems in the degenerate case. (2003) Preprint.
Helfer, A.D., Conjugate points on space like geodesics or pseudo self-adjoint Morse-Sturm-Liouville systems. Pacific J. Math. 164 (1994) 321–340. CrossRef
Jost, J., Li-Jost, X. and Peng, X.W., Bifurcation of minimal surfaces in Riemannian manifolds. Trans. Amer. Math. Soc. 347 (1995) 51–62. CrossRef
T. Kato, Perturbation Theory for linear operators. Grundlehren der Mathematischen Wissenschaften 132, Springer-Verlag (1980).
W. Klingenberg, Closed geodesics on Riemannian manifolds. CBMS Regional Conference Series in Mathematics 53 (1983).
W. Klingenberg, Riemannian Geometry. de Gruyter, New York (1995).
M.A. Krasnoselskii, Topological methods in the theory of nonlinear integral equations. Pergamon, New York (1964).
Kupeli, D.N., On conjugate and focal points in semi-Riemannian geometry. Math. Z. 198 (1988) 569–589. CrossRef
S. Lang, Differential and Riemannian Manifolds. Springer-Verlag (1995).
Meinrenken, E., Trace formulas and Conley-Zehnder index. J. Geom. Phys. 13 (1994) 1–15. CrossRef
J. Milnor, Morse theory. Based on lecture notes by M. Spivak and R. Wells. Annals of Mathematics Studies 51, Princeton University Press, Princeton, N.J. (1963).
Musso, M., Pejsachowicz, J. and Portaluri, A., Morse Index Theorem, A and bifurcation for perturbed geodesics on Semi-Riemannian Manifolds. Topol. Methods Nonlinear Anal. 25 (2005) 69–99. CrossRef
B. O'Neill, Semi-Riemannian geometry with applications to relativity. Academic Press, New York (1983).
R.S. Palais, Foundations of global non-linear analysis. W.A. Benjamin, Inc., New York (1968).
G. Peano, Lezioni di Analisi infinitesimale, Volume I, pp. 120–121, Volume II, pp. 187–195. Tipografia editrice G. Candeletti, Torino (1893).
Piccione, P., Portaluri, A. and Tausk, D.V., Spectral flow, Maslov index and bifurcation of semi-Riemannian geodesics. Ann. Global Anal. Geometry 25 (2004) 121–149. CrossRef
A. Portaluri, A formula for the Maslov index of linear autonomous Hamiltonian systems. (2004) Preprint.
A. Portaluri, Morse Index Theorem and Bifurcation theory on semi-Riemannian manifolds. Ph.D. thesis (2004).
Rabier, P.J., Generalized Jordan chains and two bifurcation theorems of Krasnosel'skii. Nonlinear Anal. 13 (1989) 903–934. CrossRef
Robbin, J. and Salamon, D., The Maslov index for paths. Topology 32 (1993) 827-844. CrossRef
Robbin, J. and Salamon, D., The spectral flow and the Maslov index. Bull. London Math. Soc. 27 (1995) 1–33. CrossRef