No CrossRef data available.
Article contents
On a Volume Constrained Variational Problem in SBV²(Ω): Part I
Published online by Cambridge University Press: 15 September 2002
Abstract
We consider the problem of minimizing the energy
$$ E(u):= \int_{\Omega}|\nabla u(x)|^2 \, {\rm d}x + \int_{S_u \cap \Omega}\left
(1 + |[u](x)|\right) \, {\rm d}H^{N - 1}(x)$$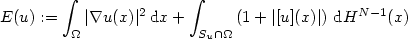
among all functions u ∈ SBV²(Ω) for which two level sets $\{u = l_i\}$
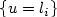have prescribed Lebesgue measure $\alpha_i$
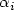. Subject to this volume constraint
the existence of minimizers for E(.) is proved and the asymptotic
behaviour of the solutions is investigated.
- Type
- Research Article
- Information
- Copyright
- © EDP Sciences, SMAI, 2002
References
L. Ambrosio, A compactness theorem for a special class of functions of bounded variation. Boll. Un. Mat. Ital.
3-B (1989) 857-881.
Ambrosio, L., Fonseca, I., Marcellini, P. and Tartar, L., On a volume constrained variational problem.
Arch. Rat. Mech. Anal.
149 (1999) 23-47.
CrossRef
Aguilera, N., Alt, H.W. and Caffarelli, L.A., An optimization problem with volume constraint.
SIAM J. Control Optim.
24 (1986) 191-198.
CrossRef
Alt, H.W. and Caffarelli, L.A., Existence and regularity for a minimum problem with free boundary.
J. Reine Angew. Math.
325 (1981) 105-144.
A. Braides and V. Chiadò-Piat, Integral representation results for functionals defined on
$SBV(\Omega; {\mathbb R}^m)$
. J. Math. Pures Appl.
75 (1996) 595-626.
. J. Math. Pures Appl.
75 (1996) 595-626.Congedo, G. and Tamanini, L., On the existence of solutions to a problem in multidimensional segmentation.
Ann. Inst. H. Poincaré Anal. Non Linéaire
2 (1991) 175-195.
CrossRef
De Giorgi, E. and Ambrosio, L., Un nuovo tipo di funzionale del calcolo delle variazioni.
Atti Accad. Naz. Lincei
82 (1988) 199-210.
G. Dal Maso, An Introduction to Γ-convergence. Birkhäuser (1993).
L.C. Evans and R.F. Gariepy, Measure Theory and Fine Properties of Functions. CRC Press, Stud. Adv. Math. (1992).
E. Giusti, Minimal Surfaces and Functions of Bounded Variation. Birkhäuser (1984).
Gurtin, M.E., Polignone, D. and Vinals, J., Two-phase binary fluids and immiscible fluids described by an order parameter.
Math. Models Methods Appl. Sci.
6 (1996) 815-831.
CrossRef
Tilli, P., On a constrained variational problem with an arbitrary number of free boundaries.
Interf. Free Boundaries
2 (2000) 201-212.
CrossRef
W. Ziemer, Weakly Differentiable Functions. Springer-Verlag (1989).