Article contents
Partial regularity of minimizers of higher order integrals with (p, q)-growth
Published online by Cambridge University Press: 23 April 2010
Abstract
We consider higher order functionals of the form
$F[u]=\int\limits_\Omega f(D^mu)\,{\rm d}x \qquad\text{for }u:\mathbb{R}^n\supset\Omega\to\mathbb{R}^N,$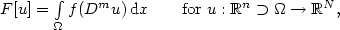
where the integrand $f:{\textstyle \bigodot^m}(\R^{n},\R^{N})\to\mathbb{R}$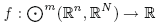 , m ≥ 1 is strictly quasiconvex and satisfies a non-standard growth condition.More precisely we assume that f fulfills the (p, q)-growth condition
, m ≥ 1 is strictly quasiconvex and satisfies a non-standard growth condition.More precisely we assume that f fulfills the (p, q)-growth condition
\[\gamma|A|^p\le f(A)\le L(1+|A|^q)\qquad \mbox{for all }A \in {\textstyle \bigodot^m}(\R^{n},\R^{N}),\]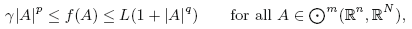
with γ, L > 0 and $1< p \le q<\min\big\{p+\frac1n,\frac{2n-1}{2n-2}p\big\}$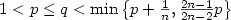 . We study minimizers of thefunctional $F[\cdot]$
. We study minimizers of thefunctional $F[\cdot]$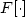 and prove a partial $C^{m,\alpha}_{\rm loc}$
and prove a partial $C^{m,\alpha}_{\rm loc}$ -regularity result.
-regularity result.
Information
- Type
- Research Article
- Information
- ESAIM: Control, Optimisation and Calculus of Variations , Volume 17 , Issue 2 , April 2011 , pp. 472 - 492
- Copyright
- © EDP Sciences, SMAI, 2010
References
Acerbi, E. and Fusco, N., Semicontinuity problems in the calculus of variations. Arch. Ration. Mech. Anal. 86 (1984) 125–145.
CrossRef
Acerbi, E. and Fusco, N., A regularity theorem for minimizers of quasiconvex integrals. Arch. Ration. Mech. Anal. 99 (1987) 261–281.
Acerbi, E. and Fusco, N., Regularity for minimizers of non-quadratic functionals: the case 1<p<2. J. Math. Anal. Appl. 140 (1989) 115–135.
CrossRef
Acerbi, E. and Fusco, N., Partial regularity under anisotropic (p, q) growth conditions. J. Differ. Equ. 107 (1994) 46–67.
CrossRef
Acerbi, E. and Mingione, G., Regularity results for a class of quasiconvex functionals with nonstandard growth. Ann. Scuola Norm. Sup. Pisa Cl. Sci. IV 30 (2001) 311–339.
Ball, J.M. and Murat, F., W 1,p-quasiconvexity and variational problems for multiple integrals. J. Funct. Anal. 58 (1984) 225–253.
CrossRef
Bildhauer, M. and Fuchs, M., Partial regularity for variational integrals with (s, µ, q)-growth. Calc. Var. Partial Differ. Equ. 13 (2001) 537–560.
CrossRef
Bildhauer, M. and Fuchs, M., C 1, α-solutions to non-autonomous anisotropic variational problems. Calc. Var. Partial Differ. Equ. 24 (2005) 309–340.
CrossRef
Bouchitté, G., Fonseca, I. and Malý, J., The effective bulk energy of the relaxed energy of multiple integrals below the growth exponent. Proc. Roy. Soc. Edinburgh Sect. A 128 (1998) 463–479.
CrossRef
Carozza, M. and Passarelli di, A. Napoli, Partial regularity for anisotropic functionals of higher order. ESAIM: COCV 13 (2007) 692–706.
CrossRef
Carozza, M., Fusco, N. and Mingione, G., Partial regularity of minimizers of quasiconvex integrals with subquadratic growth. Ann. Mat. Pura Appl. IV 175 (1998) 141–164.
CrossRef
G. Cupini, M. Guidorzi and E. Mascolo, Regularity of minimizers of vectorial integrals with p-q growth. Nonlinear Anal., Theory Methods Appl. 54 (2003) 591–616.
Duzaar, F. and Kronz, M., Regularity of ω-minimizers of quasi-convex variational integrals with polynomial growth. Differ. Geom. Appl. 17 (2002) 139–152.
CrossRef
Duzaar, F. and Steffen, K., Optimal interior and boundary regularity for almost minimizers to elliptic variational integrals. J. Reine Angew. Math. 546 (2002) 73–138.
Duzaar, F., Gastel, A. and Grotowski, J., Partial regularity for almost minimizers of quasi-convex integrals. SIAM J. Math. Anal. 32 (2000) 665–687.
CrossRef
Duzaar, F., Grotowski, J. and Kronz, M., Regularity of almost minimizers of quasi-convex variational integrals with subquadratic growth. Ann. Mat. Pura Appl. IV 184 (2005) 421–448.
CrossRef
Esposito, L. and Mingione, G., Relaxation results for higher order integrals below the natural growth exponent. Differ. Integral Equ. 15 (2002) 671–696.
Esposito, L., Leonetti, F. and Mingione, G., Regularity results for minimizers of irregular integrals with (p, q) growth. Forum Math. 14 (2002) 245–272.
Esposito, L., Leonetti, F. and Mingione, G., Sharp regularity for functionals with (p, q) growth. J. Differ. Equ. 204 (2004) 5–55.
CrossRef
Evans, L.C., Quasiconvexity and partial regularity in the calculus of variations. Arch. Ration. Mech. Anal. 95 (1986) 227–252.
Fonseca, I. and Malý, J., Relaxation of multiple integrals below the growth exponent. Ann. Inst. Henri Poincaré Anal. Non Linéaire 14 (1997) 309–338.
CrossRef
Fonseca, I. and Malý, J., From jacobian to hessian: distributional form and relaxation. Riv. Mat. Univ. Parma 4 (2005) 45–74.
Fusco, N. and Hutchinson, J., C 1, α partial regularity of functions minimising quasiconvex integrals. Manuscr. Math. 54 (1984) 121–143.
CrossRef
M. Giaquinta, Multiple integrals in the calculus of variations and nonlinear elliptic systems. Princeton University Press, Princeton (1983).
Giaquinta, M., Growth conditions and regularity, a counterexample. Manuscr. Math. 59 (1987) 245–248.
CrossRef
Giaquinta, M. and Modica, G., Partial regularity of minimizers of quasiconvex integrals. Ann. Inst. Henri Poincaré Anal. Non Linéaire 3 (1986) 185–208.
CrossRef
Guidorzi, M., A remark on partial regularity of minimizers of quasiconvex integrals of higher order. Rend. Ist. Mat. Univ. Trieste 32 (2000) 1–24.
Guidorzi, M. and Poggiolini, L., Lower semicontinuity of quasiconvex integrals of higher order. NoDEA 6 (1999) 227–246.
CrossRef
Hong, M.C., Some remarks on the minimizers of variational integrals with non standard growth conditions. Boll. Un. Mat. Ital. A 6 (1992) 91–101.
Kristensen, J., Lower semicontinuity in Sobolev spaces below the growth exponent of the integrand. Proc. Roy. Soc. Edinburgh Sect. A 127 (1997) 797–817.
CrossRef
Kristensen, J. and Mingione, G., The singular set of lipschitzian minima of multiple integrals. Arch. Ration. Mech. Anal. 184 (2007) 341–369.
CrossRef
Kronz, M., Partial regularity results for minimizers of quasiconvex functionals of higher order. Ann. Inst. Henri Poincaré Anal. Non Linéaire 19 (2002) 81–112.
CrossRef
Marcellini, P., Approximation of quasiconvex functions and lower semicontinuity of multiple integrals. Manuscr. Math. 51 (1985) 1–28.
CrossRef
Marcellini, P., On the definition and the lower semicontinuity of certain quasiconvex integrals. Ann. Inst. Henri Poincaré Anal. Non Linéaire 3 (1986) 391–409.
CrossRef
P. Marcellini, Un exemple de solution discontinue d'un problème variationnel dans le cas scalaire. Preprint Istituto Matematico U. Dini, Universita' di Firenze (1987/1988), n. 11.
Marcellini, P., Regularity of minimizers of integrals of the calculus of variations with non-standard growth conditions. Arch. Ration. Mech. Anal. 105 (1989) 267–284.
Marcellini, P., Regularity and existence of solutions of elliptic equations with p, q-growth conditions. J. Differ. Equ. 90 (1991) 1–30.
CrossRef
Marcellini, P., Everywhere regularity for a class of elliptic systems without growth conditions. Ann. Scuola Norm. Sup. Pisa Cl. Sci. IV 23 (1996) 1–25.
Meyers, N.G., Quasi-convexity and lower semi-continuity of multiple variational integrals of any order. Trans. Am. Math. Soc. 119 (1965) 125–149.
CrossRef
Morrey, C.B., Quasi-convexity and the lower semicontinuity of multiple integrals. Pac. J. Math. 2 (1952) 25–53.
CrossRef
Passarelli di, A. Napoli and F. Siepe, A regularity result for a class of anisotropic systems. Rend. Ist. Mat. Univ. Trieste 28 (1996) 13–31.
Schemm, S. and Schmidt, T., Partial regularity of strong local minimizers of quasiconvex integrals with (p, q)-growth. Proc. Roy. Soc. Edinburgh Sect. A 139 (2009) 595–621.
CrossRef
Schmidt, T., Regularity of minimizers of W 1,p-quasiconvex variational integrals with (p, q)-growth. Calc. Var. Partial Differ. Equ. 32 (2008) 1–24.
CrossRef
Schmidt, T., Regularity of relaxed minimizers of quasiconvex variational integrals with (p, q)-growth. Arch. Ration. Mech. Anal. 193 (2009) 311–337.
CrossRef
Siepe, F. and Guidorzi, M., Partial regularity for quasiconvex integrals of any order. Ric. Mat. 52 (2003) 31–54.
- 1
- Cited by

