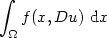Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
De Maria, Bruno
and
Passarelli di Napoli, Antonia
2011.
A new partial regularity result for non-autonomous convex integrals with non-standard growth conditions.
Journal of Differential Equations,
Vol. 250,
Issue. 3,
p.
1363.