Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T07:24:00.600Z Has data issue: false hasContentIssue false
  • English
  • Français

Relaxation in BV of integrals with superlineargrowth

Published online by Cambridge University Press:  13 August 2014

Parth Soneji
Parth Soneji*
Affiliation:
Ludwig Maximilians University Munich, Theresienstr. 39, 80333 Munich, Germany. soneji@math.lmu.de
Get access

Abstract

We study properties of the functional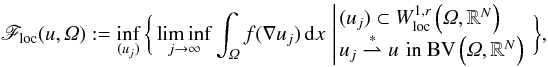

\begin{eqnarray} \mathscr{F}_{{\rm loc}}(u,\Omega):=\inf_{(u_{j})}\bigg\{ \liminf_{j\rightarrow\infty}\int_{\Omega}f(\nabla u_{j})\udx\, \left| \!\!\begin{array}{rl} & (u_{j})\subset W_{{\rmloc}}^{1,r}\left(\Omega, \RN\right) \\ & u_{j}\tostar u\,\,\textrm{in}\BV\left(\Omega, \RN\right) \end{array} \right. \bigg\}, \end{eqnarray}Floc(u,Ω):=inf(uj)lim infj→∞∫Ωf(∇uj) dx ,
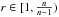where u ∈BV(Ω;RN), andf:RN ×n → R is continuous and satisfies0 ≤ f(ξ) ≤L(1 + | ξ |r). For r ∈ [1,2),assuming fhas linear growth in certain rank-one directions, we combine a result of [A. Braides andA. Coscia, Proc. Roy. Soc. Edinburgh Sect. A 124 (1994)737–756] with a new technique involving mollification to prove an upper bound forFloc. Then, for\hbox{$r\in[1,\frac{n}{n-1})$}r∈[1,nn−1), we prove thatFloc satisfiesthe lower bound
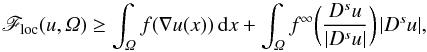\begin{equation*} \scF_{{\rm loc}}(u,\Omega) \geq \int_{\Omega}f(\nabla u (x))\ud x + \int_{\Omega}\finf\bigg(\frac{D^{s}u}{|D^{s}u|}\bigg)\,|D^{s}u|, \end{equation*}Floc(u,Ω)≥∫Ωf(∇u(x)) dx+∫Ωf∞Dsu|Dsu| |Dsu|,
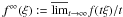 provided f is quasiconvex, and the recession functionf∞ (defined as\hbox{$ f^{\infty}(\xi):= \overline{\lim}_{t\rightarrow\infty}f(t\xi )/t$}f∞(ξ):=limt→∞f(tξ)/t) is assumed to be finite incertain rank-one directions. The proof of this result involves adapting work by[Kristensen, Calc. Var. Partial Differ. Eqs. 7 (1998)249–261], and [Ambrosio and Dal Maso, J. Funct. Anal. 109(1992) 76–97], and applying a non-standard blow-up technique that exploits fineproperties of BV maps. It also makes use of the fact that Floc has a measurerepresentation, which is proved in the appendix using a method of [Fonseca and Malý,Annal. Inst. Henri Poincaré Anal. Non Linéaire 14 (1997)309–338].

Keywords

Quasiconvexitylower semicontinuityrelaxationBV
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 20 , Issue 4 , October 2014 , pp. 1078 - 1122
Copyright
© EDP Sciences, SMAI, 2014

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acerbi, E. and Fusco, N., Semicontinuity problems in the calculus of variations. Arch. Ration. Mech. Anal. 86 (1984) 125–145. Google Scholar
Alberti, G., Rank one property for derivatives of functions with bounded variation. Proc. Roy. Soc. Edinburgh Sect. A 123 (1993) 239–274. Google Scholar
Alberti, G. and Ambrosio, L., A geometrical approach to monotone functions in Rn, Math. Z. 230 (1999) 259–316. Google Scholar
Amar, M. and De Cicco, V., Quasi-polyhedral approximation of BV-functions. Ric. Mat. 54 (2005) 485–490 (2006). Google Scholar
Ambrosio, L., A compactness theorem for a new class of functions of bounded variation. Boll. Un. Mat. Ital. B 3 (1989) 857–881. Google Scholar
Ambrosio, L., Existence theory for a new class of variational problems. Arch. Ration. Mech. Anal. 111 (1990) 291–322. Google Scholar
Ambrosio, L., On the lower semicontinuity of quasiconvex integrals in SBV(Ω, Rk). Nonlinear Anal. 23 (1994) 405–425. Google Scholar
Ambrosio, L. and Maso, G. Dal, On the relaxation in BV(Ω;Rm) of quasi-convex integrals. J. Funct. Anal. 109 (1992) 76–97. Google Scholar
Ambrosio, L., Fusco, N. and Hutchinson, J., Higher integrability of the gradient and dimension of the singular set for minimisers of the Mumford-Shah functional. Calc. Var. Partial Differ. Eq. 16 (2003) 187–215. Google Scholar
L. Ambrosio, N. Fusco, and D. Pallara, Functions of bounded variation and free discontinuity problems. Oxf. Math. Monogr. The Clarendon Press Oxford University Press, New York (2000).
Ambrosio, L., Mortola, S., and Tortorelli, V., Functionals with linear growth defined on vector valued BV functions. J. Math. Pures Appl. 70 (1991) 269–323. Google Scholar
Ambrosio, L. and Pallara, D., Integral representations of relaxed functionals on BV(Rn, Rk) and polyhedral approximation. Indiana Univ. Math. J. 42 (1993) 295–321. Google Scholar
Aviles, P. and Giga, Y., Variational integrals on mappings of bounded variation and their lower semicontinuity. Arch. Ration. Mech. Anal. 115 (1991) 201–255. Google Scholar
Ball, J. and Murat, F., W 1,p-quasiconvexity and variational problems for multiple integrals. J. Funct. Anal. 58 (1984) 225–253. Google Scholar
Bouchitté, G., Fonseca, I., and Malý, J., The effective bulk energy of the relaxed energy of multiple integrals below the growth exponent. Proc. Roy. Soc. Edinburgh Sect. A 128 (1998) 463–479. Google Scholar
Braides, A. and Coscia, A., The interaction between bulk energy and surface energy in multiple integrals. Proc. Roy. Soc. Edinburgh Sect. A 124 (1994) 737–756. Google Scholar
G. Buttazzo, Semicontinuity, relaxation and integral representation in the calculus of variations. Pitman Res. Notes in Math. Ser., vol. 207. Longman Scientific & Technical, Harlow (1989).
Carbone, L. and De Arcangelis, R., Further results on Γ-convergence and lower semicontinuity of integral functionals depending on vector-valued functions. Ric. Mat. 39 (1990) 99–129. Google Scholar
Dal Maso, G., Integral representation on BV(Ω) of Γ-limits of variational integrals. Manuscr. Math. 30 (1979/80) 387–416. Google Scholar
De Giorgi, E. and Ambrosio, L., New functionals in the calculus of variations. Atti Accad. Naz. Lincei Rend. Cl. Sci. Fis. Mat. Natur. 82 (1988) 199–210 (1989). Google Scholar
E. De Giorgi, F. Colombini, and L. Piccinini, Frontiere orientate di misura minima e questioni collegate. Scuola Normale Superiore, Pisa (1972).
L. Evans and R. Gariepy, Measure theory and fine properties of functions. Stud.Adv. Math. CRC Press, Boca Raton, FL (1992).
Fonseca, I., Lower semicontinuity of surface energies. Proc. Roy. Soc. Edinburgh Sect. A 120 (1992) 99–115. Google Scholar
Fonseca, I. and Malý, J., Relaxation of multiple integrals below the growth exponent. Annal. Inst. Henri Poincaré Anal. Non Linéaire 14 (1997) 309–338. Google Scholar
Fonseca, I. and Marcellini, P., Relaxation of multiple integrals in subcritical Sobolev spaces. J. Geom. Anal. 7 (1997) 57–81. Google Scholar
Fonseca, I. and Müller, S., Quasi-convex integrands and lower semicontinuity in L 1. SIAM J. Math. Anal. 23 (1992) 1081–1098. Google Scholar
Fonseca, I. and Müller, S., Relaxation of quasiconvex functionals in BV(Ω, Rp) for integrands f(x,u,∇u). Arch. Ration. Mech. Anal. 123 (1993) 1–49. Google Scholar
Fonseca, I. and Rybka, P., Relaxation of multiple integrals in the space BV(Ω, Rp). Proc. Roy. Soc. Edinburgh Sect. A 121 (1992) 321–348. Google Scholar
Goffman, C. and Serrin, J., Sublinear functions of measures and variational integrals. Duke Math. J. 31 (1964) 159–178. Google Scholar
Kristensen, J., Lower semicontinuity of quasi-convex integrals in BV(Ω;Rm). Calc. Var. Partial Differ. Eqs. 7 (1998) 249–261. Google Scholar
Larsen, C., Quasiconvexification in W 1,1 and optimal jump microstructure in BV relaxation. SIAM J. Math. Anal. 29 (1998) 823–848. Google Scholar
Lebesgue, H., Intégrale, longueur, aire. Ann. Mat. Pura Appl. 7 (1902) 231–359. Google Scholar
Malý, J., Weak lower semicontinuity of polyconvex and quasiconvex integrals. Manuscr. Math. 85 (1994) 419–428. Google Scholar
Marcellini, P., Approximation of quasiconvex functions, and lower semicontinuity of multiple integrals. Manuscr. Math. 51 (1985) 1–28. Google Scholar
Marcellini, P., On the definition and the lower semicontinuity of certain quasiconvex integrals. Annal. Inst. Henri Poincaré Anal. Non Linéaire 3 (1986) 391–409. Google Scholar
P. Mattila, Geometry of sets and measures in Euclidean spaces. Cambridge Stud. Adv. Math., vol. 44. Cambridge University Press, Cambridge (1995), Fractals and rectifiability.
Meyers, N., Quasi-convexity and lower semi-continuity of multiple variational integrals of any order. Trans. Amer. Math. Soc. 119 (1965) 125–149. Google Scholar
Morrey, C., Quasi-convexity and the lower semicontinuity of multiple integrals. Pacific J. Math. 2 (1952) 25–53. Google Scholar
C. Morrey, Multiple integrals in the calculus of variations. Classics Math. (1966).
Müller, S., On quasiconvex functions which are homogeneous of degree 1. Indiana Univ. Math. J. 41 (1992) 295–301. Google Scholar
Reshetnyak, J., General theorems on semicontinuity and convergence with functionals. Sibirsk. Mat. Ž. 8 (1967) 1051–1069. Google Scholar
Rindler, F., Lower semicontinuity and Young measures in BV(Ω;Rm) without Alberti’s Rank-One Theorem. Adv. Calc. Var. 5 (2012) 127–159. Google Scholar
W. Rudin, Real and complex analysis, 3rd edition, McGraw-Hill Book Co., New York (1987).
Schmidt, T., Regularity of relaxed minimizers of quasiconvex variational integrals with (p,q)-growth. Arch. Ration. Mech. Anal. 193 (2009) 311–337. Google Scholar
Schmidt, T., A simple partial regularity proof for minimizers of variational integrals. NoDEA Nonlinear Differ. Eq. Appl. 16 (2009) 109–129. Google Scholar
Serrin, J., A new definition of the integral for nonparametric problems in the calculus of variations. Acta Math. 102 (1959) 23–32. Google Scholar
Serrin, J., On the definition and properties of certain variational integrals. Trans. Amer. Math. Soc. 101 (1961) 139–167. Google Scholar
Soneji, P., Lower semicontinuity in BV of quasiconvex integrals with subquadratic growth. ESAIM: COCV 19 (2013) 555–573. Google Scholar
W. Ziemer, Weakly differentiable functions. Sobolev spaces and functions of bounded variation. Graduate Texts Math., vol. 120. Springer-Verlag, New York (1989).