Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-10T12:41:25.744Z Has data issue: false hasContentIssue false
  • English
  • Français

Relaxation of Quasilinear Elliptic Systems via A-quasiconvex Envelopes

Published online by Cambridge University Press:  15 September 2002

Uldis Raitums
Uldis Raitums*
Affiliation:
Institute of Mathematics and Computer Science, University of Latvia, 1459 Riga, Latvia; uldis.raitums@mii.lu.lv.
Get access

Abstract

We consider the weak closure WZ of the set Z of all feasible pairs (solution, flow) of the family of potential elliptic systems $$ \begin{array}{c}\mbox{div}\left(\sum\limits_{s=1}^{s_0}\sigma_s(x)F_s^\prime (\nabla u(x)+g(x))-f(x)\right)=0\;\mbox{in}\,\Omega, u=(u_1,\dots, u_m)\in H_0^1(\Omega;{\bf R}^m),\;\sigma=(\sigma_1,\dots,\sigma_{s_0})\in S,\end{array} $$ 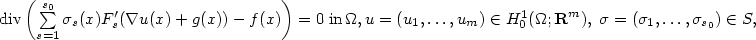where Ω ⊂ Rn is a bounded Lipschitz domain, Fs are strictly convex smooth functions with quadratic growth and $S=\{\sigma\, measurable\,\mid\,\sigma_s(x)=0\;\mbox{or}\,1,\;s=1,\dots,s_0,\;\sigma_1(x)+\cdots +\sigma_{s_0}(x)=1\}$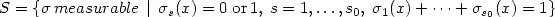. We show that WZ is the zero level set for an integral functional with the integrand $Q\cal F$ 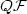being the A-quasiconvex envelope for a certain function $\cal F$ 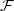and the operator A = (curl,div)m. If the functions Fs are isotropic, then on the characteristic cone Λ (defined by the operator A) $Q{\cal F}$ 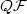coincides with the A-polyconvex envelope of $\cal F$ 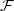and can be computed by means of rank-one laminates.

Keywords

Quasilinear elliptic systemrelaxationA-quasiconvex envelope.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 7 , 2002 , pp. 309 - 334
Copyright
© EDP Sciences, SMAI, 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

J. Ball, B. Kirchheim and J. Kristensen, Regularity of quasiconvex envelopes, Preprint No. 72/1999. Max-Planck Institute für Mathematik in der Naturwissenschaften, Leipzig (1999).
B. Dacorogna, Direct Methods in the Calculus of Variations. Springer: Berlin, Heidelberg, New York (1989).
Fonseca, I. and Müller, S., A-quasiconvexity, lower semicontinuity, and Young measures. SIAM J. Math. Anal. 30 (1999) 1355-1390. CrossRef
R.V. Kohn and G. Strang, Optimal design and relaxation of variational problems, Parts I-III. Comm. Pure Appl. Math. 39 (1986) 113-137, 138-182, 353-377.
Lurie, K.A., Fedorov, A.V. and Cherkaev, A.V., Regularization of optimal problems of design of bars and plates, Parts 1 and 2. JOTA 37 (1982) 499-543. CrossRef
Miettinen, M. and Raitums, U., On C 1-regularity of functions that define G-closure. Z. Anal. Anwendungen 20 (2001) 203-214. CrossRef
Murat, F., Compacité par compensation : condition nécessaire et suffisante de continuité faible sous une hypothèse de rang constant. Ann. Scuola Norm. Super. Pisa 8 (1981) 69-102.
U. Raitums, Properties of optimal control problems for elliptic equations, edited by W. Jäger et al., Partial Differential Equations Theory and Numerical Solutions. Boca Raton: Chapman & Hall/CRC, Res. Notes in Math. 406 (2000) 290-297.
L. Tartar, An introduction to the homogenization method in optimal design. CIME Summer Course. Troia (1998). http://www.math.cmu.edu/cna/publications.html
V.V. Zhikov, S.M. Kozlov and O.A. Oleinik, Homogenization of Differential Operators and Integral Functionals. Springer: Berlin, Hedelberg, New York (1994).