Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-10T11:50:28.719Z Has data issue: false hasContentIssue false
  • English
  • Français

Stabilization of wave systems with input delayin the boundary control

Published online by Cambridge University Press:  11 October 2006

Gen Qi Xu ,
Siu Pang Yung  and
Leong Kwan Li
Gen Qi Xu
Affiliation:
Mathematics Department of Tianjin University, Tianjin, 300072, P.R. China; gqxu@tju.edu.cn
Siu Pang Yung
Affiliation:
Mathematics Department of Hong Kong University, Hong Kong, P.R. China; spyung@hku.hk
Leong Kwan Li
Affiliation:
Applied Mathematics Department of the Hong Kong Polytechnic University, Hong Kong, P.R. China; malblkli@polyu.edu.hk
Get access

Abstract

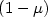In the present paper, we consider a wave system that is fixed at one end and a boundary control input possessing a partial time delay of weight $(1-\mu)$ is applied over the other end. Using a simple boundary velocity feedback law, we show that the closed loop systemgenerates a C 0 group of linear operators. After a spectral analysis, we show that the closed loop system is a Riesz one, that is, there is a sequence of eigenvectors andgeneralized eigenvectors that forms a Riesz basis for the state Hilbert space.Furthermore, we show that when the weight $\mu>\frac{1}{2}$ , for any time delay,we can choose a suitable feedback gain so that the closed loop system is exponentially stable. When $\mu=\frac{1}{2}$ 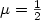, we show that the system is at most asymptotically stable. When $\mu<\frac{1}{2}$ 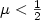, the system is always unstable.

Keywords

Wave equationtime delaystabilizationRiesz basis.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 12 , Issue 4 , October 2006 , pp. 770 - 785
Copyright
© EDP Sciences, SMAI, 2006

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

I. Gumowski and C. Mira, Optimization in Control Theory and Practice. Cambridge University Press, Cambridge (1968).
R. Datko, J. Lagness and M.P. Poilis, An example on the effect of time delays in boundary feedback stabilization of wave equations. SIAM J. Control Optim. 24 (1986) 152–156.
R. Datko, Not all feedback stabilized hyperbolic systems are robust with respect to small time delay in their feedbacks. SIAM J. Control Optim. 26 (1988) 697–713.
Suh, I.H. and Bien, Z., Use of time delay action in the controller design. IEEE Trans. Automat. Control 25 (1980) 600–603. CrossRef
Kwon, W.H., Lee, G.W. and Kim, S.W., Performance improvement, using time delays in multi-variable controller design. INT J. Control 52 (1990) 1455–1473. CrossRef
G. Abdallah, P. Dorato, J. Benitez-Read and R. Byrne, Delayed positive feedback can stabilize oscillatory systems, in ACC' 93 (American control conference), San Francisco (1993) 3106–3107.
N. Jalili and N. Olgac, Optimum delayed feedback vibration absorber for MDOF mechanical structure, in 37th IEEE CDC'98 (Conference on decision and control), Tampa, FL, December (1998) 4734–4739.
Aernouts, W., Roose, D. and Sepulchre, R., Delayed control of a Moore-Greitzer axial compressor model. Intern. J. Bifurcation Chaos 10 (2000) 115–1164.
Hale, J.K. and Verduyn-Lunel, S.M., Strong stabilization of neutral functional differential equations. IMA J. Math. Control Inform. 19 (2002) 5–24. CrossRef
J.K. Hale and S.M. Verduyn-Lunel, Introduction to functional differential equations, in Applied Mathematical Sciences, New York, Springer 99 (1993).
Niculescu, S.I. and Lozano, R., On the passivity of linear delay systems. IEEE Trans. Automat. Control 46 (2001) 460–464. CrossRef
P. Borne, M. Dambrine, W. Perruquetti and J.P. Richard, Vector Lyapunov functions: nonlinear, time-varying, ordinary and functional differential equations. Stability and control: theory, methods and applications 13, Taylor and Francis, London (2003) 49–73.
Mörgul, Ö., On the stabilization and stability robustness against small delays of some damped wave equation. IEEE Trans. Automat. Control 40 (1995) 1626–1630. CrossRef
Mörgul, Ö., Stabilization and disturbance rejection for the wave equation. IEEE Trans. Automat. Control 43 (1998) 89–95. CrossRef
Lions, J.-L., Exact controllability, stabilization and perturbations for distributed parameter system. SIAM Rev. 30 (1988) 1–68. CrossRef
Xu, G.Q. and Guo, B.Z., Riesz basis property of evolution equations in Hilbert spaces and application to a coupled string equation. SIAM J. Control Optim. 42 (2003) 966–984. CrossRef
Shubov, M.A., The Riesz basis property of the system of root vectors for the equation of a nonhomogeneous damped string: transformation operators method. Methods Appl. Anal. 6 (1999) 571–591.
Xu, G.Q. and Yung, S.P., The expansion of semigroup and a criterion of Riesz basis. J. Differ. Equ. 210 (2005) 1–24. CrossRef
I.C. Gohberg and M.G. Krein, Introduction to the Theory of Linear Nonselfadjoint Operators. AMS Transl. Math. Monographs 18 (1969).
Lars V. Ahlfors, Complex Analysis. McGraw-Hill.