Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T22:17:46.040Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniform estimates for the parabolic Ginzburg–Landau equation

Published online by Cambridge University Press:  15 August 2002

F. Bethuel  and
G. Orlandi
F. Bethuel
Affiliation:
Analyse Numerique, Université P. et M. Curie, BC 187, 4 place Jussieu 75252 Paris Cedex 05, France; bethuel@ann.jussieu.fr.
G. Orlandi
Affiliation:
Dipartimento di Informatica, Università di Verona, strada le Grazie, 37134 Verona, Italy.
Get access

Abstract

We consider complex-valued solutions uE of the Ginzburg–Landau equation on a smooth bounded simply connected domain Ω of $\mathbb{R}^N$ 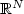, N ≥ 2, where ε > 0 is a small parameter. We assume that the Ginzburg–Landau energy $E_\varepsilon(u_\varepsilon)$ 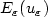verifies the bound (natural in the context) $E_\varepsilon(u_\varepsilon)\le M_0|\log\varepsilon|$ 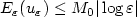, where M 0 is some given constant. We also make several assumptions on the boundary data. An important step in the asymptotic analysis of uE, as ε → 0, is to establish uniform Lp bounds for the gradient, for some p>1. We review some recent techniques developed in the elliptic case in [7], discuss some variants, and extend the methods to the associated parabolic equation.

Keywords

Ginzburg–Landauparabolic equationsHodge–de RhamdecompositionJacobians.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 8: A tribute to JL Lions , 2002 , pp. 219 - 238
Copyright
© EDP Sciences, SMAI, 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

G. Alberti, S. Baldo and G. Orlandi, Variational convergence for functionals of Ginzburg-Landau type. Preprint (2001).
L. Almeida, S. Baldo, F. Bethuel and G. Orlandi (in preparation).
Almeida, L. and Bethuel, F., Topological methods for the Ginzburg-Landau equation. J. Math. Pures Appl. 11 (1998) 1-49. CrossRef
Ambrosio, L. and Soner, H.M., A measure theoretic approach to higher codimension mean curvature flow. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 25 (1997) 27-49.
Baumann, P., Chen, C.-N., Phillips, D. and Sternberg, P., Vortex annihilation in nonlinear heat flow for Ginzburg-Landau systems. Eur. J. Appl. Math. 6 (1995) 115-126.
F. Bethuel, Variational methods for Ginzburg-Landau equations, in Calculus of Variations and Geometric evolution problems, Cetraro 1996, edited by S. Hildebrandt and M. Struwe. Springer (1999).
Bethuel, F., Bourgain, J., Brezis, H. and Orlandi, G., W 1,p estimates for solutions to the Ginzburg-Landau equation with boundary data in H 1/2. C. R. Acad. Sci. Paris Sér. I Math. 333 (2001) 1069-1076. CrossRef
Bethuel, F., Brezis, H. and Hélein, F., Asymptotics for the minimization of a Ginzburg-Landau functional. Calc. Var. Partial Differential Equations 1 (1993) 123-148. CrossRef
F. Bethuel, H. Brezis and F. Hélein, Ginzburg-Landau Vortices. Birkhäuser, Boston (1994).
Bethuel, F., Brezis, H. and Orlandi, G., Small energy solutions to the Ginzburg-Landau equation. C. R. Acad. Sci. Paris Sér. I Math. 331 (2000) 763-770. CrossRef
Bethuel, F., Brezis, H. and Orlandi, G., Asymptotics for the Ginzburg-Landau equation in arbitrary dimensions. J. Funct. Anal. 186 (2001) 432-520. Erratum (to appear). CrossRef
Bethuel, F. and Rivière, T., Vortices for a variational problem related to superconductivity. Ann. Inst. H. Poincaré Anal. Non Linéaire 12 (1995) 243-303. CrossRef
Bourgain, J., Brezis, H. and Mironescu, P., Lifting in Sobolev spaces. J. Anal. 80 (2000) 37-86.
Bourgain, J., Brezis, H. and Mironescu, P., On the structure of the Sobolev space H 1/2 with values into the circle. C. R. Acad. Sci. Paris Sér. I Math. 331 (2000) 119-124. CrossRef
Brezis, H. and Mironescu, P., Sur une conjecture de E. De Giorgi relative à l'énergie de Ginzburg-Landau. C. R. Acad. Sci. Paris Sér. I Math. 319 (1994) 167-170.
H. Federer, Geometric Measure Theory. Springer, Berlin (1969).
Han, Z.C. and Shafrir, I., Lower bounds for the energy of S 1-valued maps in perforated domains. J. Anal. Math. 66 (1995) 295-305. CrossRef
R. Hardt and F.H. Lin, Mappings minimizing the L p -norm of the gradient. Comm. Pure Appl. Math. 40 (1987) 555-588. CrossRef
Jerrard, R., Lower bounds for generalized Ginzburg-Landau functionals. SIAM J. Math. Anal. 30 (1999) 721-746. CrossRef
Jerrard, R. and Soner, H.M., Dynamics of Ginzburg-Landau vortices. Arch. Rational Mech. Anal. 142 (1998) 99-125. CrossRef
Jerrard, R. and Soner, H.M., Scaling limits and regularity results for a class of Ginzburg-Landau systems. Ann. Inst. H. Poincaré Anal. Non Linéaire 16 (1999) 423-466. CrossRef
R. Jerrard and H.M. Soner, The Jacobian and the Ginzburg-Landau energy. Calc. Var. Partial Differential Equations (to appear).
Lin, F.H., Some dynamical properties of Ginzburg-Landau vortices. Comm. Pure Appl. Math. 49 (1996) 323-359. 3.0.CO;2-E>CrossRef
F.H. Lin, Complex Ginzburg-Landau equations and dynamics of vortices, filaments, and codimension-2 submanifolds. Comm. Pure Appl. Math. 51 (1998) 385-441
F.H. Lin, Rectifiability of defect measures, fundamental groups and density of Sobolev mappings, in Journées ``Équations aux Dérivées Partielles", Saint-Jean-de-Monts, 1996, Exp. No. XII. École Polytechnique, Palaiseau (1996).
Lin, F.H. and Rivière, T., Complex Ginzburg-Landau equations in high dimensions and codimension two area minimizing currents. J. Eur. Math. Soc. 1 (1999) 237-311. Erratum, Ibid. CrossRef
Lin, F.H. and Rivière, T., A quantization property for static Ginzburg-Landau vortices. Comm. Pure Appl. Math. 54 (2001) 206-228. 3.0.CO;2-W>CrossRef
Lin, F.H. and Rivière, T., A quantization property for moving line vortices. Comm. Pure Appl. Math. 54 (2001) 826-850.
L. Modica, The gradient theory of phase transitions and the minimal interface criterion. Arch. Rational Mech. Anal. 98 (1987) 123-142.
Modica, L. and Mortola, S., Un esempio di Γ-convergenza. Boll. Un. Mat. Ital. B 14 (1977) 285-299.
Rivière, T., Line vortices in the U(1)-Higgs model. ESAIM: COCV 1 (1996) 77-167. CrossRef
Rivière, T., Dense subsets of H 1/2(S 2,S 1). Ann. Global Anal. Geom. 18 (2000) 517-528. CrossRef
Rivière, T., Asymptotic analysis for the Ginzburg-Landau Equation. Boll. Un. Mat. Ital. B 8 (1999) 537-575.
E. Sandier, Lower bounds for the energy of unit vector fields and applications. J. Funct. Anal. 152 (1997) 379-403; Erratum 171 (2000) 233.
L. Simon, Lectures on Geometric Measure Theory, in Proc. of the Centre for Math. Analysis. Australian Nat. Univ., Canberra (1983).
M. Struwe, On the asymptotic behavior of the Ginzburg-Landau model in 2 dimensions. J. Differential Equations 7 (1994) 1613-1624; Erratum 8 (1995) 224.