Hostname: page-component-7dd5485656-c8zdz Total loading time: 0 Render date: 2025-10-28T17:35:48.032Z Has data issue: false hasContentIssue false
  • English
  • Français

Analysis of gradient flow of a regularized Mumford-Shahfunctional for image segmentation and image inpainting

Published online by Cambridge University Press:  15 March 2004

Xiaobing Feng  and
Andreas Prohl
Xiaobing Feng
Affiliation:
Department of Mathematics, The University of Tennessee, Knoxville, TN 37996, USA.
Andreas Prohl
Affiliation:
Department of Mathematics, ETHZ, 8092 Zürich, Switzerland, apr@math.ethz.ch.
Get access

Abstract

This paper studies the gradient flow of a regularized Mumford-Shah functionalproposed by Ambrosio and Tortorelli (1990, 1992) for image segmentation, and adopted by Esedoglu and Shen (2002) for image inpainting. It is shown that the gradient flow with L2 x L∞ initial data possesses a global weak solution, and it has a unique global in timestrong solution, which has at most finite number of point singularities in the space-time, when the initial data are in H1 x H1 ∩ L∞ . A family of fully discrete approximation schemes using low order finite elements is proposed for the gradient flow. Convergence of a subsequence (resp. the whole sequence)of the numerical solutions to a weak solution (resp. the strong solution) of the gradient flow is established as the mesh sizes tend to zero, and optimal and suboptimal order error estimates, which depend on $\frac{1}{{\varepsilon}}$ 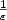and $\frac{1}{k_{\varepsilon}}$ 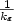only in low polynomial order, are derived for the proposed fully discrete schemes under the mesh relation $k=o(h^{\frac12})$ 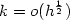. Numerical experiments are also presented to show effectiveness of the proposed numerical methods and to validate the theoretical analysis.

Keywords

Image segmentation and inpaintingMumford-Shah modelelliptic approximationgradient flowa priori estimatesfinite element methoderror analysis.

Information

Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 38 , Issue 2 , March 2004 , pp. 291 - 320
Copyright
© EDP Sciences, SMAI, 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

R.A. Adams, Sobolev Spaces. Academic Press, New York (1975).
Ambrosio, L. and Tortorelli, V.M., Approximation of functionals depending on jumps by elliptic functionals via Γ-convergence. Comm. Pure Appl. Math. 43 (1990) 999–1036. CrossRef
L. Ambrosio and V.M. Tortorelli, On the approximation of functionals depending on jumps by quadratic, elliptic functionals. Boll. Un. Mat. Ital. 6-B (1992) 105–123.
L. Ambrosio, N. Fusco and D. Pallara, Functions of Bounded Variation and Free Discontinuity Problems. Oxford University Press (2000).
J.W. Barrett, X. Feng and A. Prohl, Convergence of a fully discrete finite element method for a degenerate parabolic system modeling nematic liquid crystals with variable degree of orientation, preprint.
Bellettini, G. and Coscia, A., Discrete approximation of a free discontinuity problem. Numer. Funct. Anal. Optimiz. 15 (1994) 201–224. CrossRef
A. Blake and A. Zisserman, Visual reconstruction. MIT Press, Cambridge, MA (1987).
Bourdin, B., Image segmentation with a finite element method. ESAIM: M2AN 33 (1999) 229–244. CrossRef
A. Braides, Approximation of free-discontinuity problems. Lect. Notes Math. 1694, Springer-Verlag (1998).
Braides, A. and Dal Maso, G., Nonlocal approximation of the Mumford-Shah functional. Calc. Var. Partial Differential Equations 5 (1997) 293–322. CrossRef
S.C. Brenner and L.R. Scott, The Mathematical Theory of Finite Element Methods, Second Edition, Springer-Verlag, New York (2001).
Cahn, J.W. and Hilliard, J.E., Free energy of a nonuniform system I, Interfacial free energy. J. Chem. Phys. 28 (1958) 258–267. CrossRef
Chambolle, A., Image segmentation by variational methods: Mumford-Shah functional and the discrete approximation. SIAM J. Appl. Math. 55 (1995) 827–863. CrossRef
Chambolle, A. and Dal Maso, G., Discrete approximation of the Mumford-Shah functional in dimension two. ESAIM: M2AN 33 (1999) 651–672. CrossRef
P.G. Ciarlet, Basic error estimates for elliptic problems, in Handbook of Numer. Anal. II, Elsevier Sciences Publishers (1991).
G. Dal Maso, An introduction to Γ-convergence, Birkhäuser Boston, Boston, MA (1993).
De Giorgi, E., Carriero, M. and Leaci, A., Existence theorem for a minimum problem with discontinuity set. Arch. Rat. Mech. Anal. 108 (1989) 195–218.
De Giorgi, E. and Franzoni, T., Su un tipo di convergenza variazionale. Atti Accad. Naz. Lincei Rend. Cl. Sci. Fis. Mat. Natur. 58 (1975) 842–850.
F. Dibos and E. Séré, An approximation result for the minimizers of the Mumford-Shah functional. Boll. Un. Mat. Ital. A 11 (1997).
Elliott, C.M., French, D.A. and Milner, F.A., A second order splitting method for the Cahn-Hilliard equation. Numer. Math. 54 (1989) 575–590. CrossRef
Esedoglu, S. and Shen, J., Digital inpainting based on the Mumford-Shah-Euler image model. European J. Appl. Math. 13 (2002) 353–370. CrossRef
Feng, X. and Prohl, A., Analysis of total variation flow and its finite element approximations. ESAIM: M2AN 37 (2003) 533–556. CrossRef
X. Feng and A. Prohl, On gradient flow of the Mumford-Shah functional. (in preparation).
Geman, D. and Geman, S., Stochastic relaxation, Gibbs distributions and the Bayesian restoration of images. IEEE Trans. Patten Anal. Mach. Intell. 6 (1984) 721–741. CrossRef
R. Glowinski, J.L. Lions and R. Trémoliéres, Numerical analysis of variational inequalities. North-Holland, New York. Stud. Math. Appl. 8 (1981).
Gobbino, M., Gradient flow for the one-dimensional Mumford-Shah strategies. Ann. Scuola Norm. Sup. Pisa Cl. Sci. 27 (1998) 145–193.
J.L. Lions, Quelques méthodes de résolution des problèmes aux limites non linéaires, Dunod (1969).
March, R. and Dozio, M., A variational method for the recovery of smooth boundaries. Im. Vis. Comp. 15 (1997) 705–712.
Modica, L., The gradient theory of phase transitions and the minimal interface criterion. Arch. Rational Mech. Anal. 98 (1987) 123–142. CrossRef
Modica, L. and Mortola, S., Un esempio di Γ-convergenza. Boll. Un. Mat. Ital. B 14 (1977) 285–299.
J.-M. Morel and S. Solimini, Variational Methods in Image Segmentation, Birkhäuser (1995).
Mumford, D. and Shah, J., Optimal approximations by piecewise smooth functions and associated variational problems. Comm. Pure Appl. Math. 42 (1989) 577–685. CrossRef
Nochetto, R.H. and Verdi, C., Convergence past singularities for a fully discrete approximation of curvature-driven interfaces. SIAM J. Numer. Anal. 34 (1997) 490–512. CrossRef
Simon, J., Compact sets in the space Lp(0,T;B). Ann. Mat. Pura Appl. 146 (1987) 65–96. CrossRef
Struwe, M., Geometric evolution problems. IAS/Park City Math. Series 2 (1996) 259–339.