Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-10T17:14:36.890Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximation of solutions of Hamilton-Jacobi equationson the Heisenberg group

Published online by Cambridge University Press:  27 May 2008

Yves Achdou  and
Italo Capuzzo-Dolcetta
Yves Achdou
Affiliation:
UFR Mathématiques, Université Paris 7, Case 7012, 75251 Paris Cedex 05, France. Laboratoire Jacques-Louis Lions, Université Paris 6, 75252 Paris Cedex 05, France. achdou@math.jussieu.fr
Italo Capuzzo-Dolcetta
Affiliation:
Dipartimento di Matematica, Università Roma “La Sapienza”, Piazzale A. Moro 2, 00185 Roma, Italy. capuzzo@mat.uniroma1.it
Get access

Abstract

We propose and analyze numerical schemes for viscosity solutions of time-dependent Hamilton-Jacobi equations on the Heisenberg group.The main idea is to construct a grid compatible with the noncommutative group geometry. Under suitable assumptions on the data, the Hamiltonian and the parameters for the discrete first order scheme,we prove that the error between the viscosity solution computed at the grid nodes and the solution of the discrete problem behaves like $\sqrt{h}$ 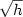where h is the mesh step. Such an estimate is similar to those available in the Euclidean geometrical setting.The theoretical results are tested numerically on some examples for which semi-analytical formulas for the computation of geodesics are known. Other simulations are presented, for both steady and unsteady problems.

Keywords

Degenerate Hamilton-Jacobi equationHeisenberg groupfinite difference schemeserror estimates.
Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 42 , Issue 4 , July 2008 , pp. 565 - 591
Copyright
© EDP Sciences, SMAI, 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Achdou, Y. and Tchou, N., A finite difference scheme on a non commutative group. Numer. Math. 89 (2001) 401–424. CrossRef
Bardi, M., A boundary value problem for the minimum-time function. SIAM J. Control Optim. 27 (1989) 776–785. CrossRef
M. Bardi and I. Capuzzo-Dolcetta, Optimal control and viscosity solutions of Hamilton-Jacobi-Bellman equations, Systems & Control: Foundations & Applications. Birkhäuser Boston Inc., Boston, MA (1997). With appendices by M. Falcone and P. Soravia.
Barles, G. and Jakobsen, E.R., Error bounds for monotone approximation schemes for Hamilton-Jacobi-Bellman equations. SIAM J. Numer. Anal. 43 (2005) 540–558 (electronic). CrossRef
Beals, R., Gaveau, B. and Greiner, P.C., Hamilton-Jacobi theory and the heat kernel on Heisenberg groups. J. Math. Pures Appl. 79 (2000) 633–689. CrossRef
A. Bellaïche and J.-J. Risler, Eds., Sub-Riemannian Geometry, Progress in Mathematics 144. Birkhäuser Verlag, Basel (1996).
Birindelli, I. and Wigniolle, J., Homogenization of Hamilton-Jacobi equations in the Heisenberg group. Commun. Pure Appl. Anal. 2 (2003) 461–479.
R.W. Brockett, Control theory and singular Riemannian geometry, in New directions in applied mathematics (Cleveland, Ohio, 1980), Springer, New York (1982) 11–27.
Capuzzo Dolcetta, I., On a discrete approximation of the Hamilton-Jacobi equation of dynamic programming. Appl. Math. Optim. 10 (1983) 367–377. CrossRef
Capuzzo Dolcetta, I., The Hopf-Lax solution for state dependent Hamilton-Jacobi equations (Viscosity solutions of differential equations and related topics) (Japanese). Sūrikaisekikenkyūsho Kōkyūroku 1287 (2002) 143–154.
I. Capuzzo Dolcetta, The Hopf solution of Hamilton-Jacobi equations, in Elliptic and parabolic problems (Rolduc/Gaeta, 2001), World Sci. Publishing, River Edge, NJ (2002) 343–351.
I. Capuzzo Dolcetta, A generalized Hopf-Lax formula: analytical and approximations aspects, in Geometric Control and Nonsmooth Analysis, F. Ancona, A. Bressan, P. Cannarsa, F. Clarkeă and P.R. Wolenski Eds., Series on Advances in Mathematics for Applied Sciences 76, World Scientific Publishing Co. Pte. Ltd., Hackensack, NJ (2008).
Capuzzo Dolcetta, I. and Ishii, H., Approximate solutions of the Bellman equation of deterministic control theory. Appl. Math. Optim. 11 (1984) 161–181. CrossRef
Crandall, M.G. and Lions, P.-L., Two approximations of solutions of Hamilton-Jacobi equations. Math. Comp. 43 (1984) 1–19. CrossRef
Cutrí, A. and Da Lio, F., Comparison and existence results for evolutive non-coercive first-order Hamilton-Jacobi equations. ESAIM: COCV 13 (2007) 484–502. CrossRef
Engquist, B. and Osher, S., One-sided difference approximations for nonlinear conservation laws. Math. Comp. 36 (1981) 321–351. CrossRef
Falcone, M., A numerical approach to the infinite horizon problem of deterministic control theory. Appl. Math. Optim. 15 (1987) 1–13. CrossRef
Falcone, M. and Ferretti, R., Discrete time high-order schemes for viscosity solutions of Hamilton-Jacobi-Bellman equations. Numer. Math. 67 (1994) 315–344. CrossRef
Gottlieb, S., Shu, C.-W. and Tadmor, E., Strong stability-preserving high-order time discretization methods. SIAM Rev. 43 (2001) 89–112 (electronic). CrossRef
Harten, A., Engquist, B., Osher, S. and Chakravarthy, S.R., Uniformly high-order accurate essentially nonoscillatory schemes. III. J. Comput. Phys. 71 (1987) 231–303. CrossRef
Korányi, A. and Reimann, H.M., Quasiconformal mappings on the Heisenberg group. Invent. Math. 80 (1985) 309–338. CrossRef
Krylov, N.V., On the rate of convergence of finite-difference approximations for Bellman's equations with variable coefficients. Probab. Theory Relat. Fields 117 (2000) 1–16. CrossRef
Krylov, N.V., The rate of convergence of finite-difference approximations for Bellman equations with Lipschitz coefficients. Appl. Math. Optim. 52 (2005) 365–399. CrossRef
Manfredi, J.J. and Stroffolini, B., A version of the Hopf-Lax formula in the Heisenberg group. Comm. Partial Diff. Eq. 27 (2002) 1139–1159. CrossRef
Osher, S. and Sethian, J.A., Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations. J. Comput. Phys. 79 (1988) 12–49. CrossRef
Osher, S. and Shu, C.-W., High-order essentially nonoscillatory schemes for Hamilton-Jacobi equations. SIAM J. Numer. Anal. 28 (1991) 907–922. CrossRef
J.A. Sethian, Level set methods and fast marching methods, Evolving interfaces in computational geometry, fluid mechanics, computer vision, and materials science, Cambridge Monographs on Applied and Computational Mathematics 3. Cambridge University Press, Cambridge, 2nd edition (1999).