Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-29T02:21:58.422Z Has data issue: false hasContentIssue false
  • English
  • Français

New unilateral problems in stratigraphy

Published online by Cambridge University Press:  15 November 2006

Stanislav N. Antontsev ,
Gérard Gagneux ,
Robert Luce  and
Guy Vallet
Stanislav N. Antontsev
Affiliation:
Departamento de Matemática, Universidade da Beira Interior Covilhã 6201-001, Portugal. anton@ubi.pt
Gérard Gagneux
Affiliation:
Laboratoire de Mathématiques Appliquées UMR-CNRS 5142 IPRA  BP 1155, 64 013 Pau Cedex, France. gerard.gagneux@univ-pau.fr; robert.luce@univ-pau.fr; guy.vallet@univ-pau.fr
Robert Luce
Affiliation:
Laboratoire de Mathématiques Appliquées UMR-CNRS 5142 IPRA  BP 1155, 64 013 Pau Cedex, France. gerard.gagneux@univ-pau.fr; robert.luce@univ-pau.fr; guy.vallet@univ-pau.fr
Guy Vallet
Affiliation:
Laboratoire de Mathématiques Appliquées UMR-CNRS 5142 IPRA  BP 1155, 64 013 Pau Cedex, France. gerard.gagneux@univ-pau.fr; robert.luce@univ-pau.fr; guy.vallet@univ-pau.fr
Get access

Abstract

This work deals with the study of some stratigraphic models for the formation of geological basins under a maximal erosion rate constrain. It leads to introduce differentialinclusions of degenerated hyperbolic-parabolic type $0\in \partial _{t}u-div\{H(\partial _{t}u+E)\nabla u\}$ 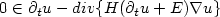, where H is the maximal monotonous graph of the Heaviside function and E is a given non-negative function. Firstly, we present the new and realistic models and an original mathematical formulation, taking into account the weather-limited rate constraint in the conservation law, with a unilateral constraint on the outflow boundary. Then, we give a study of the 1-D case with numerical illustrations.

Keywords

Stratigraphic modelsweather limiteddegenerated parabolic-hyperbolic conservation laws.
Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 40 , Issue 4 , July 2006 , pp. 765 - 784
Copyright
© EDP Sciences, SMAI, 2006

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

S.N. Antontsev, D. Etienne, G. Gagneux and G. Vallet, New unilateral problems in stratigraphy. Publication interne du Laboratoire de Mathématiques Appliquées, UMR-CNRS 5142, Université de Pau, No. 05/13 (2005).
S.N. Antontsev, G. Gagneux, R. Luce and G. Vallet, Weather limited constraint in stratigraphy. International conference “Tikhonov and Contemporary Mathematics": section 5, Mathematical Geophysics, Moscow (2006) 7–8.
S.N. Antontsev, G. Gagneux and G. Vallet, Analyse mathématique d'un modèle d'asservissement stratigraphique. Approche gravitationnelle d'un processus de sédimentation sous contrainte d'érosion maximale. Publication interne du Laboratoire de Mathématiques Appliquées, UMR-CNRS 5142, Université de Pau, No. 01/23 (2001).
S.N. Antontsev, G. Gagneux and G. Vallet, On some stratigraphic control problems, Prikladnaya Mekhanika Tekhnicheskaja Fisika (Novosibirsk) 44 (2003) 85–94 (in Russian), and Journal of Applied Mechanics and Technical Physics (New York) 44 (2003) 821–828. CrossRef
P. Bénilan, M.G. Crandall and A. Pazy, Bonnes solutions d'un problème d'évolution semi-linéaire. C. R. Acad. Sci. Paris Sér. I Math. (306) (1988) 527–530.
Cuesta, C., van Duijn, C.J. and Hulshof, J., Infiltration in porous media with dynamic capillary pressure: Travelling waves. Eur. J. Appl. Math. 11 (2000) 381–397. CrossRef
D. Etienne, Contribution à l'analyse mathématique de modèles stratigraphiques. Thèse de l'Université de Pau, France (2004).
Eymard, R. and Gallouët, T., Analytical and numerical study of a model of erosion and sedimentation. SIAM J. Numer. Anal. 43 (2006) 2344–2370. CrossRef
Eymard, R., Gallouët, T., Granjeon, D., Masson, R. and Tran, Q.H., Multi-lithology stratigraphic model under maximum erosion rate constraint. Internat. J. Numer. Methods Engrg. 60 (2004) 527–548. CrossRef
G. Gagneux, R. Luce and G. Vallet, A non-standard free-boundary problem arising from stratigraphy. Publication interne du Laboratoire de Mathématiques Appliquées, UMR-CNRS 5142, Université de Pau, No. 04/33 (2004).
G. Gagneux and M. Madaune-Tort, Analyse mathématique de modèles non linéaires de l'ingénierie pétrolière. Mathématiques & Applications, Vol. 22 Springer, Paris (1996).
G. Gagneux and G. Vallet, Sur des problèmes d'asservissements stratigraphiques. ESAIM: COCV “A tribute to Jacques-Louis Lions” 8 (2002) 715–739.
G. Gagneux and G. Vallet, A result of existence for an original convection-diffusion equation. Revista de la Real Academia de Ciencias, Serie A: Matemáticas (RACSAM) 99 (2005) 125–131.
T. Gallouët, Equations satisfaites par des limites de solutions approchées, conférence plénière, 34ème congrès d'analyse numérique, Anglet (Pyrénées Atlantiques), in Canum (2002) 87–96.
Gervais, V. and Masson, R., Mathematical and numerical analysis of a stratigraphic model. ESAIM: M2AN 38 (2004) 585-611. CrossRef
J.-L. Lions, Cours d'Analyse Numérique. Hermann, École Polytechnique, Paris (1973).
J.-L. Lions, Quelques méthodes de résolution des problèmes aux limites non linéaires. Dunod, Paris (1969).
G. Vallet, Sur une loi de conservation issue de la géologie. C. R. Acad. Sci. Paris Sér. I Math. (337) (2003) 559–564.