Article contents
On the two-dimensional compressible isentropic Navier–Stokes equations
Published online by Cambridge University Press: 15 January 2003
Abstract
We analyze the compressible isentropic Navier–Stokes equations (Lions, 1998) in the two-dimensional case with $\gamma=\displaystyle{{c_{p}}/{c_{v}}}=2$ 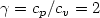 . These equations also modelizethe shallow water problem in height-flow rate formulation used tosolve the flow in lakes and perfectly well-mixed sea. We establisha convergence result for the time-discretized problem when themomentum equation and the continuity equation are solved with theGalerkin method, without adding a penalization term in thecontinuity equation as it is made in Lions (1998). The secondpart is devoted to the numerical analysis and mainly deals withproblems of geophysical fluids. We compare the simulationsobtained with this compressible isentropic Navier–Stokes model andthose obtained with a shallow water model (Di Martino et al., 1999). At first,the computations are executed on a simplified domain in order tovalidate the method by comparison with existing numerical resultsand then on a real domain: the dam of Calacuccia (France). At last, we numerically implement an analyticalexample presented by Weigant (1995) which shows thateven if the data are rather smooth, we cannot have bounds onρ in Lp for p large if $\gamma<2$
. These equations also modelizethe shallow water problem in height-flow rate formulation used tosolve the flow in lakes and perfectly well-mixed sea. We establisha convergence result for the time-discretized problem when themomentum equation and the continuity equation are solved with theGalerkin method, without adding a penalization term in thecontinuity equation as it is made in Lions (1998). The secondpart is devoted to the numerical analysis and mainly deals withproblems of geophysical fluids. We compare the simulationsobtained with this compressible isentropic Navier–Stokes model andthose obtained with a shallow water model (Di Martino et al., 1999). At first,the computations are executed on a simplified domain in order tovalidate the method by comparison with existing numerical resultsand then on a real domain: the dam of Calacuccia (France). At last, we numerically implement an analyticalexample presented by Weigant (1995) which shows thateven if the data are rather smooth, we cannot have bounds onρ in Lp for p large if $\gamma<2$ 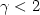 when N=2.
when N=2.
Information
- Type
- Research Article
- Information
- ESAIM: Mathematical Modelling and Numerical Analysis , Volume 36 , Issue 6 , November 2002 , pp. 1091 - 1109
- Copyright
- © EDP Sciences, SMAI, 2002
References
- 1
- Cited by

