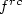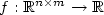Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bartels, Sören
2005.
Reliable and Efficient Approximation of Polyconvex Envelopes.
SIAM Journal on Numerical Analysis,
Vol. 43,
Issue. 1,
p.
363.
Bartels, Sören
Carstensen, Carsten
Conti, Sergio
Hackl, Klaus
Hoppe, Ulrich
and
Orlando, Antonio
2006.
Analysis, Modeling and Simulation of Multiscale Problems.
p.
197.
Carstensen, Carsten
and
Huth, Robert
2008.
IUTAM Symposium on Theoretical, Computational and Modelling Aspects of Inelastic Media.
Vol. 11,
Issue. ,
p.
41.
Bartels, Sören
and
Kružík, Martin
2011.
An Efficient Approach to the Numerical Solution of Rate-Independent Problems with Nonconvex Energies.
Multiscale Modeling & Simulation,
Vol. 9,
Issue. 3,
p.
1276.
Dolzmann, G.
2013.
Microstructure and effective behavior of materials.
ZAMM - Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik,
Vol. 93,
Issue. 1,
p.
4.
Bartels, Sören
2015.
Numerical Methods for Nonlinear Partial Differential Equations.
Vol. 47,
Issue. ,
p.
261.
Conti, Sergio
and
Dolzmann, Georg
2017.
Analytical and Numerical Tools for Relaxation in Crystal Plasticity.
Procedia IUTAM,
Vol. 20,
Issue. ,
p.
56.
Benešová, Barbora
and
Kružík, Martin
2017.
Weak Lower Semicontinuity of Integral Functionals and Applications.
SIAM Review,
Vol. 59,
Issue. 4,
p.
703.
Oberman, Adam M.
and
Ruan, Yuanlong
2017.
A Partial Differential Equation for the Rank One Convex Envelope.
Archive for Rational Mechanics and Analysis,
Vol. 224,
Issue. 3,
p.
955.
Conti, Sergio
and
Dolzmann, Georg
2018.
An adaptive relaxation algorithm for multiscale problems and application to nematic elastomers.
Journal of the Mechanics and Physics of Solids,
Vol. 113,
Issue. ,
p.
126.
Martin, Robert J.
Voss, Jendrik
Ghiba, Ionel-Dumitrel
Sander, Oliver
and
Neff, Patrizio
2020.
The Quasiconvex Envelope of Conformally Invariant Planar Energy Functions in Isotropic Hyperelasticity.
Journal of Nonlinear Science,
Vol. 30,
Issue. 6,
p.
2885.
Li, Wenbo
and
Nochetto, Ricardo
2021.
Two-scale methods for convex envelopes.
Mathematics of Computation,
Vol. 91,
Issue. 333,
p.
111.
Köhler, Maximilian
Neumeier, Timo
Melchior, Jan
Peter, Malte A.
Peterseim, Daniel
and
Balzani, Daniel
2022.
Adaptive convexification of microsphere-based incremental damage for stress and strain softening at finite strains.
Acta Mechanica,
Vol. 233,
Issue. 11,
p.
4347.
Behr, Florian
Dolzmann, Georg
Hackl, Klaus
and
Jezdan, Ghina
2023.
Analytical and numerical relaxation results for models in soil mechanics.
Continuum Mechanics and Thermodynamics,
Vol. 35,
Issue. 5,
p.
2019.
Köhler, Maximilian
Neumeier, Timo
Peterseim, Daniel
Peter, Malte A.
and
Balzani, Daniel
2023.
Relaxed Incremental Formulations for Damage at Finite Strains Including Strain Softening.
PAMM,
Vol. 23,
Issue. 1,
Köhler, M.
Neumeier, T.
Peter, M.A.
Peterseim, D.
and
Balzani, D.
2024.
Hierarchical rank-one sequence convexification for the relaxation of variational problems with microstructures.
Computer Methods in Applied Mechanics and Engineering,
Vol. 432,
Issue. ,
p.
117321.
Balzani, D.
Köhler, M.
Neumeier, T.
Peter, M. A.
and
Peterseim, D.
2024.
Multidimensional rank-one convexification of incremental damage models at finite strains.
Computational Mechanics,
Vol. 73,
Issue. 1,
p.
27.