Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-28T12:40:33.351Z Has data issue: false hasContentIssue false
  • English
  • Français

Mathematical and numerical analysisof a stratigraphic model

Published online by Cambridge University Press:  15 August 2004

Véronique Gervais  and
Roland Masson
Véronique Gervais
Affiliation:
Institut Français du Pétrole, 1 et 4 avenue de Bois Préau, 92852 Rueil Malmaison Cedex, France. veronique.gervais@ifp.fr.
Roland Masson
Affiliation:
Institut Français du Pétrole, 1 et 4 avenue de Bois Préau, 92852 Rueil Malmaison Cedex, France. veronique.gervais@ifp.fr.
Get access

Abstract

In this paper, we consider a multi-lithology diffusion model used in stratigraphic modelling to simulate large scale transport processes of sediments described as a mixture of L lithologies. This model is a simplified one for which the surficial fluxes are proportional to the slope of the topography and to a lithology fraction with unitary diffusion coefficients.The main unknowns of the system are the sediment thickness h, the L surface concentrations $c_i^s$ 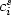in lithology i of the sediments at the top of the basin, and the L concentrations c i in lithology i of the sediments inside the basin. For this simplified model, the sediment thickness decouples from the other unknowns and satisfies a linear parabolic equation. The remaining equations account for the mass conservation of the lithologies, and couple, for each lithology, a first order linear equation for $c_i^s$ 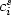with a linear advection equation for c i for which $c_i^s$ 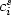appears as an input boundary condition. For this coupled system, a weak formulation is introduced which is shown to have a unique solution. An implicit finite volume scheme is derived for which we show stability estimates and the convergence to the weak solution of the problem.

Keywords

Finite volume methodstratigraphic modellinglinear first order equationsconvergence analysislinear advection equationunique weak solutionadjoint problem.
Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 38 , Issue 4 , July 2004 , pp. 585 - 611
Copyright
© EDP Sciences, SMAI, 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

R.S. Anderson and N.F. Humphrey, Interaction of Weathering and Transport Processes in the Evolution of Arid Landscapes, in Quantitative Dynamics Stratigraphy, T.A. Cross Ed., Prentice Hall (1989) 349–361.
Bardos, C., Problèmes aux limites pour les équations aux dérivées partielles du premier ordre à coefficients réels ; théorèmes d'approximation ; application à l'équation de transport. Ann. Sci. École Norm. Sup. 3 (1971) 185–233. CrossRef
Blouza, A., Le Dret, H., An up-to-the boundary version of Friedrichs' lemma and applications to the linear Koiter shell model. SIAM J. Math. Anal. 33 (2001) 877–895. CrossRef
R. Eymard, T. Gallouët, V. Gervais and R. Masson, Convergence of a numerical scheme for stratigraphic modeling. SIAM J. Numer. Anal. submitted.
Eymard, R., Gallouët, T., Granjeon, D., Masson, R. and Tran, Q.H., Multi-lithology stratigraphic model under maximum erosion rate constraint. Int. J. Numer. Meth. Eng. 60 (2004) 527–548. CrossRef
Flemings, P.B. and Jordan, T.E., A synthetic stratigraphic model of foreland basin development. J. Geophys. Res. 94 (1989) 3851–3866. CrossRef
E. Godlewski and P.A. Raviart, Numerical Approximation of Hyperbolic Systems of Conservation Laws. Springer (1996).
D. Granjeon, Modélisation Stratigraphique Déterministe: Conception et Applications d'un Modèle Diffusif 3D Multilithologique. Ph.D. Thesis, Géosciences Rennes, Rennes, France (1997).
D. Granjeon and P. Joseph, Concepts and applications of a 3D multiple lithology, diffusive model in stratigraphic modeling, in J.W. Harbaugh et al. Eds., Numerical Experiments in Stratigraphy, SEPM Sp. Publ. 62 (1999).
P.M. Kenyon and D.L. Turcotte, Morphology of a delta prograding by bulk sediment transport, Geological Society of America Bulletin 96 (1985) 1457–1465. 2.0.CO;2>CrossRef
O. Ladyzenskaja, V. Solonnikov and N. Ural'ceva, Linear and quasilinear equations of parabolic type. Transl. Math. Monogr. 23 (1968).
Rivenaes, J.C., Application of a dual lithology, depth-dependent diffusion equation in stratigraphic simulation. Basin Research 4 (1992) 133–146. CrossRef
Rivenaes, J.C., Impact of sediment transport efficiency on large-scale sequence architecture: results from stratigraphic computer simulation. Basin Research 9 (1997) 91–105. CrossRef
D.M. Tetzlaff and J.W. Harbaugh, Simulating Clastic Sedimentation. Van Norstrand Reinhold, New York (1989).
Tucker, G.E. and Slingerland, R.L., Erosional dynamics, flexural isostasy, and long-lived escarpments: A numerical modeling study. J. Geophys. Res. 99 (1994) 229–243. CrossRef