Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T05:52:10.108Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical analysis of a transmission problem with Signorini contactusing mixed-FEM and BEM*

Published online by Cambridge University Press:  21 February 2011

Gabriel N. Gatica ,
Matthias Maischak  and
Ernst P. Stephan
Gabriel N. Gatica
Affiliation:
CIMA and Departamento de Ingeniería Matemática, Universidad de Concepción, Casilla 160-C, Concepción, Chile. ggatica@ing-mat.udec.cl
Matthias Maischak
Affiliation:
BICOM, Brunel University, UB8 3PH, Uxbridge, UK. matthias.maischak@brunel.ac.uk
Ernst P. Stephan
Affiliation:
Institut für Angewandte Mathematik, Leibniz Universität Hannover, Welfengarten 1, 30167 Hannover, Germany. stephan@ifam.uni-hannover.de
Get access

Abstract

This paper is concerned with the dual formulation of the interface problemconsisting of a linear partial differential equation with variable coefficientsin some bounded Lipschitz domain Ω in $\mathbb{R}^n$ 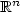(n ≥ 2) and the Laplace equation with some radiation condition in theunbounded exterior domain Ωc := $\mathbb{R}^n\backslash\bar\Omega$ 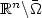. The two problems are coupled by transmission andSignorini contact conditions on the interface Γ = ∂Ω. The exterior part of theinterface problem is rewritten using a Neumann to Dirichlet mapping (NtD) given in terms of boundary integral operators. The resulting variational formulation becomes a variational inequalitywith a linear operator. Then we treat the corresponding numerical scheme and discuss anapproximation of the NtD mapping with an appropriatediscretization of the inverse Poincaré-Steklov operator. In particular, assuming some abstract approximationproperties and a discrete inf-sup condition, we show unique solvability of the discrete scheme andobtain the corresponding a-priori error estimate. Next, we prove that these assumptions aresatisfied with Raviart-Thomas elements and piecewise constants in Ω, and continuous piecewise linear functions on Γ. We suggest a solver based on a modified Uzawa algorithm and show convergence. Finally we present some numerical results illustrating our theory.

Keywords

Raviart-Thomas spaceboundary integral operatorLagrange multiplier
Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 45 , Issue 4 , July 2011 , pp. 779 - 802
Copyright
© EDP Sciences, SMAI, 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

I. Babuška and A.K. Aziz, Survey Lectures on the Mathematical Foundations of the Finite Element Method. Academic Press, New York (1972) 3–359.
Babuska, I. and Gatica, G.N., On the mixed finite element method with Lagrange multipliers. Numer. Methods Partial Differ. Equ. 19 (2003) 192–210. CrossRef
F. Brezzi and M. Fortin, Mixed and Hybrid Finite Element Methods. Springer-Verlag (1991).
Brezzi, F., Hager, W.W. and Raviart, P.-A., Error estimates for the finite element solution of variational inequalities. Numer. Math. 28 (1977) 431–443. CrossRef
Carstensen, C., Interface problem in holonomic elastoplasticity. Math. Methods Appl. Sci. 16 (1993) 819–835. CrossRef
Carstensen, C. and Gwinner, J., BEM, FEM coupling for a nonlinear transmission problem with Signorini contact. SIAM J. Numer. Anal. 34 (1997) 1845–1864. CrossRef
R. Dautray and J.-L. Lions, Mathematical Analysis and Numerical Methods for Science and Technology 4. Springer (1990).
G. Duvaut and J. Lions, Inequalities in Mechanics and Physics. Springer, Berlin (1976).
I. Ekeland and R. Temam, Analyse Convexe et Problèmes Variationnels. Études mathématiques, Dunod, Gauthier-Villars, Paris-Bruxelles-Montreal (1974).
Falk, R.S., Error estimates for the approximation of a class of variational inequalities. Math. Comput. 28 (1974) 963–971. CrossRef
Gatica, G. and Wendland, W., Coupling of mixed finite elements and boundary elements for linear and nonlinear elliptic problems. Appl. Anal. 63 (1996) 39–75. CrossRef
R. Glowinski, J.-L. Lions and R. Trémolières, Numerical Analysis of Variational Inequalities, Studies in Mathematics and its Applications 8. North-Holland Publishing Co., Amsterdam-New York (1981).
I. Hlaváček, J. Haslinger, J. Nečas and J. Lovišek, Solution of Variational Inequalities in Mechanics, Applied Mathematical Sciences 66. Springer-Verlag (1988).
L. Hörmander, Linear Partial Differential Operators. Springer-Verlag, Berlin (1969).
N. Kikuchi and J. Oden, Contact Problems in Elasticity: a Study of Variational Inequalities and Finite Element Methods. SIAM, Philadelphia (1988).
D. Kinderlehrer and G. Stampacchia, An Introduction to Variational Inequalities and their Applications. Academic Press (1980).
J. Lions and E. Magenes, Non-Homogeneous Boundary Value Problems and Applications I. Springer-Verlag, Berlin (1972).
J.E. Roberts and J.M. Thomas, Mixed and Hybrid Methods, in Handbook of Numerical Analysis II, P.G. Ciarlet and J.-L. Lions Eds., North-Holland, Amsterdam (1991) 523–639.
Z.-H. Zhong, Finite Element Procedures for Contact-Impact Problems. Oxford University Press (1993).