Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-28T00:26:24.079Z Has data issue: false hasContentIssue false
  • English
  • Français

Simultaneous vs. non-simultaneous blow-up in numerical approximations of aparabolic system with non-linear boundary conditions

Published online by Cambridge University Press:  15 April 2002

Gabriel Acosta ,
Julián Fernández Bonder ,
Pablo Groisman  and
Julio Daniel Rossi
Gabriel Acosta
Affiliation:
Instituto de Ciencias, Univ. Nac. Gral. Sarmiento, J.M. Gutierrez entre Verdi y J.L. Suarez (1613), Los Polvorines, Buenos Aires, Argentina. gacosta@ungs.edu.ar.
Julián Fernández Bonder
Affiliation:
Departamento de Matemática, FCEyN, UBA (1428), Buenos Aires, Argentina. jfbonder@dm.uba.ar. andjrossi@dm.uba.ar.
Pablo Groisman
Affiliation:
Universidad de San Andrés, Vito Dumas 284 (1644), Victoria, Buenos Aires, Argentina. pgroisman@udesa.edu.ar.
Julio Daniel Rossi
Affiliation:
Departamento de Matemática, FCEyN, UBA (1428), Buenos Aires, Argentina. jfbonder@dm.uba.ar. andjrossi@dm.uba.ar.
Get access

Abstract

We study the asymptotic behavior of a semi-discrete numerical approximation for a pair of heat equations ut = Δu, vt = Δv in Ω x (0,T); fully coupled by the boundary conditions $\frac{\partial u}{\partial\eta} = u^{p_{11}}v^{p_{12}}$ 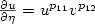, $\frac{\partial v}{\partial\eta} = u^{p_{21}}v^{p_{22}}$ 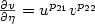on ∂Ω x (0,T), where Ω is a bounded smooth domain in ${\mathbb{R}}^d$ . We focus in the existence or not of non-simultaneous blow-up for a semi-discrete approximation (U,V). We prove that if U blows up in finite time then V can fail to blow up if and only if p 11 > 1 and p 21 < 2(p 11 - 1), which is the same condition as the one for non-simultaneous blow-up in the continuous problem. Moreover, we find that if the continuous problem has non-simultaneous blow-up then the same is true for the discrete one. We also prove some results about the convergence of the scheme and the convergence of the blow-up times.

Keywords

Blow-upparabolic equationssemi-discretization in spaceasymptotic behaviornon-linear boundary conditions.
Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 36 , Issue 1 , January 2002 , pp. 55 - 68
Copyright
© EDP Sciences, SMAI, 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abia, L.M., Lopez-Marcos, J.C. and Martinez, J., Blow-up for semidiscretizations of reaction diffusion equations. Appl. Numer. Math. 20 (1996) 145-156. CrossRef
L.M. Abia, J.C. Lopez-Marcos and J. Martinez, On the blow-up time convergence of semidiscretizations of reaction diffusion equations. Appl. Numer. Math. 26 (1998) 399-414.
G. Acosta, J. Fernández Bonder, P. Groisman and J.D. Rossi. Numerical approximation of a parabolic problem with nonlinear boundary condition in several space dimensions. Preprint.
Amann, H., Parabolic evolution equations and nonlinear boundary conditions, J. Differential Equations. 72 (1988) 201-269. CrossRef
Bandle, C. and Brunner, H., Blow-up in diffusion equations: a survey. J. Comput. Appl. Math. 97 (1998) 3-22. CrossRef
Berger, M. and Kohn, R.V., A rescaling algorithm for the numerical calculation of blowing up solution. Comm. Pure Appl. Math. 41 (1988) 841-863. CrossRef
Budd, C.J., Huang, W. and Russell, R.D., Moving mesh methods for problems with blow-up. SIAM J. Sci. Comput. 17 (1996) 305-327. CrossRef
Chen, Y.G., Asymptotic behaviours of blowing up solutions for finite difference analogue of $u_t = u_{xx} + u^{1+ \alpha}$ . J. Fac. Sci. Univ. Tokyo Sect. IA Math. 33 (1986) 541-574.
P.G. Ciarlet, The Finite Element Method for Elliptic Problems. North-Holland Publishing Company, Amsterdam, New York, Oxford (1978).
Durán, R.G., Etcheverry, J.I. and Rossi, J.D., Numerical approximation of a parabolic problem with a nonlinear boundary condition. Discrete Contin. Dyn. Syst. 4 (1998) 497-506.
Elliot, C.M. and Stuart, A.M., Global dynamics of discrete semilinear parabolic equations. SIAM J. Numer. Anal. 30 (1993) 1622-1663. CrossRef
Fernández Bonder, J. and Rossi, J.D., Blow-up vs. spurious steady solutions. Proc. Amer. Math. Soc. 129 (2001) 139-144. CrossRef
A.R. Humphries, D.A. Jones and A.M. Stuart, Approximation of dissipative partial differential equations over long time intervals, in D.F. Griffiths et al., Eds., Numerical Analysis 1993. Proc. 15th Dundee Biennal Conf. on Numerical Analysis, June 29-July 2nd, 1993, University of Dundee, UK, in Pitman Res. Notes Math. Ser. 303, Longman Scientific & Technical, Harlow (1994) 180-207.
C.V. Pao, Nonlinear Parabolic and Elliptic Equations. Plenum Press, New York (1992).
Pinasco, J.P. and Rossi, J.D., Simultaneousvs. non-simultaneous blow-up. N. Z. J. Math. 29 (2000) 55-59.
Rossi, J.D., On existence and nonexistence in the large for an N-dimensional system of heat equations with nontrivial coupling at the boundary. N. Z. J. Math. 26 (1997) 275-285.
A. Samarski, V.A. Galaktionov, S.P. Kurdyunov and A.P. Mikailov, Blow-up in QuasiLinear Parabolic Equations, in Walter de Gruyter, Ed., de Gruyter Expositions in Mathematics 19, Berlin (1995).
A.M. Stuart and A.R. Humphries, Dynamical systems and numerical analysis, in Cambridge Monographs on Applied and Computational Mathematics 2, Cambridge University Press, Cambridge (1998).