Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-10T13:53:28.275Z Has data issue: false hasContentIssue false
  • English
  • Français

Wavelet compression of anisotropic integrodifferential operators on sparse tensor product spaces

Published online by Cambridge University Press:  09 October 2009

Nils Reich
Nils Reich*
Affiliation:
ETH Zurich, Seminar for Applied Mathematics, 8092 Zurich, Switzerland. reich@math.ethz.ch
Get access

Abstract

For a class of anisotropic integrodifferential operators ${\cal B}$ 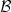arising as semigroup generators of Markov processes, we present a sparse tensor product wavelet compression scheme for the Galerkin finite element discretization of the corresponding integrodifferential equations ${\cal B}$ 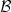u = f on [0,1]n with possibly large n. Under certain conditions on ${\cal B}$ 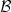, the scheme is of essentially optimal and dimension independent complexity $\mathcal{O}$ (h -1| log h |2(n-1)) without corrupting the convergence or smoothness requirements of the original sparse tensor finite element scheme. 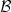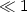If the conditions on ${\cal B}$ are not satisfied, thecomplexity can be bounded by $\mathcal{O}$ (h -(1+ε)), whereε $\ll 1$ tends to zero with increasing number of the wavelets' vanishing moments. Here h denotes the width of the corresponding finite element mesh. The operators under consideration are assumed to be of non-negative (anisotropic) order and admit a non-standard kernel κ $(\cdot,\cdot)$ 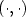that can be singular on all secondary diagonals. Practical examples of such operators from Mathematical Finance are given and some numerical results are presented.

Keywords

Wavelet compressionsparse gridsanisotropic integrodifferential operatorsnorm equivalences
Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 44 , Issue 1 , January 2010 , pp. 33 - 73
Copyright
© EDP Sciences, SMAI, 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Achdou, Y. and Pironneau, O., A numerical procedure for calibration of volatility with American options. Appl. Math. Finance 12 (2005) 201–241. CrossRef
Achdou, Y. and Tchou, N., Variational analysis for the Black and Scholes equation with stochastic volatility. ESAIM: M2AN 36 (2002) 373–395. CrossRef
Barndorff-Nielsen, O.E. and Shephard, N., Non-Gaussian Ornstein-Uhlenbeck-based models and some of their uses in financial economics. J. Roy. Stat. Soc. 63 (2001) 167–241. CrossRef
J. Bertoin, Lévy processes. Cambridge University Press, Cambridge, UK (1996).
Beylkin, G., Coifman, R. and Rokhlin, V., The fast wavelet transform and numerical algorithms. Comm. Pure Appl. Math. 44 (1991) 141–183. CrossRef
J.H. Bramble, A. Cohen and W. Dahmen, Multiscale problems and methods in numerical simulations, Lecture Notes in Mathematics 1825. Springer-Verlag, Berlin, Germany (2003).
Bungartz, H.-J. and Griebel, M., A note on the complexity of solving Poisson's equation for spaces of bounded mixed derivatives. J. Complexity 15 (1999) 167–199. CrossRef
Cohen, A., Daubechies, I. and Feauveau, J.-C., Biorthogonal bases of compactly supported wavelets. Comm. Pure Appl. Math. 45 (1992) 485–560. CrossRef
Cohen, A., Dahmen, W. and DeVore, R., Adaptive wavelet methods for elliptic operator equations: convergence rates. Math. Comp. 70 (2001) 27–75 (electronic). CrossRef
Cohen, A., Dahmen, W. and DeVore, R., Adaptive wavelet methods. II. Beyond the elliptic case. Found. Comput. Math. 2 (2002) 203–245. CrossRef
R. Cont and P. Tankov, Financial modelling with jump processes. Chapman & Hall/CRC Financial Mathematics Series. Chapman & Hall/CRC, Boca Raton, USA (2004).
Cont, R. and Voltchkova, E., A finite difference scheme for option pricing in jump diffusion and exponential Lévy models. SIAM J. Numer. Anal. 43 (2005) 1596–1626. CrossRef
Dahmen, W. and Schneider, R., Wavelets with complementary boundary conditions – function spaces on the cube. Results Math. 34 (1998) 255–293. CrossRef
Dahmen, W., Prössdorf, S. and Schneider, R., Wavelet approximation methods for pseudodifferential equations. II. Matrix compression and fast solution. Adv. Comput. Math. 1 (1993) 259–335. CrossRef
W. Dahmen, S. Prössdorf and R. Schneider, Multiscale methods for pseudo-differential equations on smooth closed manifolds, in Wavelets: theory, algorithms, and applications (Taormina, 1993), Wavelet Anal. Appl. 5, Academic Press, San Diego, USA (1994) 385–424.
Dahmen, W., Kunoth, A. and Urban, K., Biorthogonal spline wavelets on the interval – stability and moment conditions. Appl. Comput. Harmon. Anal. 6 (1999) 132–196. CrossRef
Dahmen, W., Harbrecht, H. and Schneider, R., Compression techniques for boundary integral equations – asymptotically optimal complexity estimates. SIAM J. Numer. Anal. 43 (2006) 2251–2271 (electronic). CrossRef
Delbaen, F. and Schachermayer, W., A general version of the fundamental theorem of asset pricing. Math. Ann. 300 (1994) 463–520. CrossRef
Delbaen, F. and Schachermayer, W., The variance-optimal martingale measure for continuous processes. Bernoulli 2 (1996) 81–105. CrossRef
Delbaen, F., Grandits, P., Rheinländer, T., Samperi, D., Schweizer, M. and Stricker, C., Exponential hedging and entropic penalties. Math. Finance 12 (2002) 99–123. CrossRef
M. Demuth and J. van Casteren, Stochastic Spectral Theory for Selfadjoint Feller Operators. Birkhäuser Verlag, Basel (2000).
R. DeVore, Nonlinear approximation, in Acta numerica (1998), Acta Numer. 7, Cambridge Univ. Press, Cambridge, UK (1998) 51–150.
A. Ern and J.-L. Guermond, Theory and practice of Finite Elements. Springer Verlag, New York, USA (2004).
Farkas, W., Reich, N. and Schwab, C., Anisotropic stable Lévy copula processes – analytical and numerical aspects. Math. Models Methods Appl. Sci. 17 (2007) 1405–1443. CrossRef
Gantumur, T. and Stevenson, R., Computation of differential operators in wavelet coordinates. Math. Comp. 75 (2006) 697–709 (electronic). CrossRef
Gantumur, T., Harbrecht, H. and Stevenson, R., An optimal adaptive wavelet method without coarsening of the iterands. Math. Comp. 76 (2007) 615–629 (electronic). CrossRef
M. Griebel and S. Knapek, Optimized general sparse grid approximation spaces for operator equations. Math. Comp. (to appear).
Griebel, M., Oswald, P. and Schiekofer, T., Sparse grids for boundary integral equations. Numer. Math. 83 (1999) 279–312. CrossRef
H. Harbrecht and R. Schneider, Biorthogonal wavelet bases for the boundary element method. Math. Nachr. 269/270 (2004) 167–188.
Harbrecht, H. and Schneider, R., Wavelet Galerkin schemes for boundary integral equations – implementation and quadrature. SIAM J. Sci. Comput. 27 (2006) 1347–1370 (electronic). CrossRef
Hilber, N., Matache, A.-M. and Schwab, C., Sparse wavelet methods for option pricing under stochastic volatility. J. Comput. Finance 8 (2005) 1–42. CrossRef
Hilber, N., Reich, N., Schwab, C. and Winter, C., Numerical methods for Lévy processes. Finance Stoch. 13 (2009) 471–500. Special Issue on Computational Methods in Finance (Part II). CrossRef
N. Hilber, N. Reich and C. Winter, Wavelet methods, in Encyclopedia of Quantitative Finance, R. Cont Ed., John Wiley & Sons Ltd., Chichester (to appear).
W. Hoh, Pseudo Differential Operators generating Markov Processes. Habilitationsschrift, University of Bielefeld, Germany (1998).
L. Hörmander, Linear partial differential operators, Grundlehren der Mathematischen Wissenschaften 116 [Fundamental Principles of Mathematical Sciences]. Springer-Verlag, Berlin, Germany (1963).
L. Hörmander, The analysis of linear partial differential operators. III: Pseudodifferential operators, Grundlehren der Mathematischen Wissenschaften 274 [Fundamental Principles of Mathematical Sciences]. Springer-Verlag, Berlin, Germany (1985).
N. Jacob, Pseudo Differential Operators and Markov Processes, Vol. 2: Generators and their potential theory. Imperial College Press, London, UK (2002).
N. Jacob, Pseudo Differential Operators and Markov Processes, Vol. 3: Markov processes and applications. Imperial College Press, London, UK (2005).
S. Knapek and F. Koster, Integral operators on sparse grids. SIAM J. Numer. Anal. 39 (2001/2002) 1794–1809 (electronic).
F. Liu, N. Reich and A. Zhou, Two-scale Finite Element Discretizations for Infinitesimal Generators of Jump Processes in Finance. Research report 2008-23 Seminar for Applied Mathematics, ETH Zürich, Switzerland (2008).
Matache, A.-M., von Petersdorff, T. and Schwab, C., Fast deterministic pricing of options on Lévy driven assets. ESAIM: M2AN 38 (2004) 37–71. CrossRef
Matache, A.-M., Nitsche, P.A. and Schwab, C., Wavelet Galerkin pricing of American contracts on Lévy driven assets. Quant. Finance 5 (2005) 403–424. CrossRef
Nguyen, H. and Stevenson, R., Finite element wavelets on manifolds. IMA J. Numer. Math. 23 (2003) 149–173. CrossRef
P. Oswald, On N-term approximation by Haar functions in H s -norms, in Metric Function Theory and Related Topics in Analysis, S.M. Nikolskij, B.S. Kashin and A.D. Izaak Eds., AFC, Moscow, Russia (1999) 137–163.
N. Reich, Multiscale analysis for jump processes in finance, in Numerical Mathematics and Advanced Applications, K. Kunisch, G. Of and O. Steinbach Eds., Springer Verlag, Berlin, Germany (2008) 415–422.
N. Reich, Wavelet Compression of Anisotropic Integrodifferential Operators on Sparse Tensor Product Spaces. Ph.D. Thesis 17661, ETH Zürich, Switzerland (2008). Available at http://e-collection.ethbib.ethz.ch/view/eth:30174.
N. Reich, Wavelet Compression of Integral Operators on Sparse Tensor Spaces – Construction, Consistency and Asymptotically Optimal Complexity. Research report 2008-24, Seminar for Applied Mathematics, ETH Zürich, Switzerland (2008).
Reich, N., Anisotropic operator symbols arising from multivariate jump processes. Integr. Equ. Oper. Theory 63 (2009) 127–150. CrossRef
N. Reich, C. Schwab and C. Winter, On Kolmogorov equations for anisotropic multivariate Lévy processes. Finance Stoch. (to appear).
K.-I. Sato, Lévy Processes and Infinitely Divisible Distributions. Cambridge University Press, Cambridge, UK (1999).
R. Schneider, Multiskalen- und Wavelet-Matrixkompression: Analysisbasierte Methoden zur Lösung großer vollbesetzter Gleichungssysteme. B.G. Teubner, Stuttgart, Germany (1998).
Schwab, C. and Stevenson, R., Adaptive wavelet algorithms for elliptic PDE's on product domains. Math. Comp. 77 (2008) 71–92 (electronic). CrossRef
R.E. Showalter, Monotone Operators in Banach Space and Nonliner Partial Differential Equations. American Mathematical Society, Rhode Island, USA (1997).
E.M. Stein, Harmonic Analysis. Princeton University Press, Princeton, USA (1993).
Stevenson, R., On the compressibility of operators in wavelet coordinates. SIAM J. Math. Anal. 35 (2004) 1110–1132 (electronic). CrossRef
M.E. Taylor, Pseudodifferential operators. Princeton University Press, Princeton, USA (1981).
H. Triebel, Interpolation theory, function spaces, differential operators. Second edition, Johann Ambrosius Barth Verlag, Heidelberg, Germany (1995).
T. von Petersdorff and C. Schwab, Fully discrete multiscale Galerkin BEM, in Multiscale wavelet methods for PDEs, W. Dahmen, A. Kurdila and P. Oswald Eds., Academic Press, San Diego, USA (1997) 287–346.
von Petersdorff, T. and Schwab, C., Wavelet discretizations of parabolic integrodifferential equations. SIAM J. Numer. Anal. 41 (2003) 159–180 (electronic). CrossRef
von Petersdorff, T. and Schwab, C., Numerical solution of parabolic equations in high dimensions. ESAIM: M2AN 38 (2004) 93–127. CrossRef
von Petersdorff, T., Schwab, C. and Schneider, R., Multiwavelets for second-kind integral equations. SIAM J. Numer. Anal. 34 (1997) 2212–2227. CrossRef
C. Winter, Wavelet Galerkin schemes for option pricing in multidimensional Lévy models. Ph.D. Thesis 18221, ETH Zürich, Switzerland (2009). Available at http://e-collection.ethbib.ethz.ch/view/eth:41555.