Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bartels, S.
Carstensen, C.
Hackl, K.
and
Hoppe, U.
2004.
Effective relaxation for microstructure simulations: algorithms and applications.
Computer Methods in Applied Mechanics and Engineering,
Vol. 193,
Issue. 48-51,
p.
5143.
Rieger, Marc Oliver
2005.
Elliptic and Parabolic Problems.
Vol. 63,
Issue. ,
p.
403.
Prohl, Andreas
2008.
Convergence of a Finite Element-Based Space-Time Discretization in Elastodynamics.
SIAM Journal on Numerical Analysis,
Vol. 46,
Issue. 5,
p.
2469.
Amorim, Paulo
and
Antontsev, Stanislav
2013.
Young measure solutions for the wave equation withp(x,t)-Laplacian: Existence and blow-up.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 92,
Issue. ,
p.
153.
Antontsev, S.
and
Ferreira, J.
2013.
Existence, uniqueness and blowup for hyperbolic equations with nonstandard growth conditions.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 93,
Issue. ,
p.
62.
Emmrich, Etienne
and
Šiška, David
2013.
Evolution equations of second order with nonconvex potential and linear damping: existence via convergence of a full discretization.
Journal of Differential Equations,
Vol. 255,
Issue. 10,
p.
3719.
Emmrich, Etienne
and
Puhst, Dimitri
2015.
Survey of Existence Results in Nonlinear Peridynamics in Comparison with Local Elastodynamics.
Computational Methods in Applied Mathematics,
Vol. 15,
Issue. 4,
p.
483.
Xiang, Mingqi
2015.
Young measure solutions for a fourth-order wave equation with variable growth.
Boundary Value Problems,
Vol. 2015,
Issue. 1,
Nguyen, Hong Thai
and
Paͅczka, Dariusz
2016.
Weak and Young Measure Solutions for Hyperbolic Initial Boundary Value Problems of Elastodynamics in the Orlicz--Sobolev Space Setting.
SIAM Journal on Mathematical Analysis,
Vol. 48,
Issue. 2,
p.
1297.
Kim, Seonghak
and
Koh, Youngwoo
2019.
Two-Phase Solutions for One-Dimensional Non-convex Elastodynamics.
Archive for Rational Mechanics and Analysis,
Vol. 232,
Issue. 1,
p.
489.
Hynd, Ryan
2022.
Newton’s second law with a semiconvex potential.
Partial Differential Equations and Applications,
Vol. 3,
Issue. 1,
Roubíček, Tomáš
2024.
Thermodynamics of viscoelastic solids, its Eulerian formulation, and existence of weak solutions.
Zeitschrift für angewandte Mathematik und Physik,
Vol. 75,
Issue. 2,
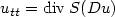 with the non-monotone stress-strain relation $S=D\phi$
with the non-monotone stress-strain relation $S=D\phi$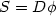 plus proper boundary and initial conditions. This hyperbolic-elliptic
initial-boundary value problem of changing types allows, in general,
solely Young-measure solutions. This paper introduces a
fully-numerical time-space discretization of this equation in a
corresponding very weak sense. It is shown that discrete solutions
exist and generate weakly convergent subsequences whose limit is
a Young-measure solution. Numerical examples in one space
dimension illustrate the time-evolving phase transitions and microstructures of a nonlinearly
vibrating string.
plus proper boundary and initial conditions. This hyperbolic-elliptic
initial-boundary value problem of changing types allows, in general,
solely Young-measure solutions. This paper introduces a
fully-numerical time-space discretization of this equation in a
corresponding very weak sense. It is shown that discrete solutions
exist and generate weakly convergent subsequences whose limit is
a Young-measure solution. Numerical examples in one space
dimension illustrate the time-evolving phase transitions and microstructures of a nonlinearly
vibrating string.