Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T06:45:48.093Z Has data issue: false hasContentIssue false
  • English
  • Français

Adaptive tests of qualitative hypotheses

Published online by Cambridge University Press:  15 May 2003

Yannick Baraud ,
Sylvie Huet  and
Béatrice Laurent
Yannick Baraud
Affiliation:
École Normale Supérieure, DMA, 45 rue d'Ulm, 75230 Paris Cedex 05, France; yannick.baraud@ens.fr.
Sylvie Huet
Affiliation:
Unité BIA, 78352 Jouy-en-Josas Cedex, France; Sylvie.Huet@jouy.inra.fr.
Béatrice Laurent
Affiliation:
bâtiment 425, Université Paris-Sud, 91405 Orsay Cedex, France; beatrice.laurent@math.u-psud.fr.
Get access

Abstract

We propose a test of a qualitative hypothesis on the mean of a n-Gaussianvector. The testing procedure is available when the variance of theobservations is unknown and does not depend on any prior information onthe alternative. The properties of the test are non-asymptotic. Fortesting positivity or monotonicity, weestablish separation rates with respect to the Euclidean distance, oversubsets of $\mathbb{R}^{n}$ 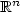which are related to Hölderian balls in functionalspaces. We provide a simulation study in order to evaluate theprocedure when the purpose is to test monotonicity in a functionalregression model and to check the robustness of the procedure tonon-Gaussian errors.

Keywords

Adaptive testtest of monotonicitytest of positivityqualitative hypothesis testingnonparametric alternativenonparametric regression.
Type
Research Article
Information
ESAIM: Probability and Statistics , Volume 7 , March 2003 , pp. 147 - 159
Copyright
© EDP Sciences, SMAI, 2003

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baraud, Y., Model selection for regression on a fixed design. Probab. Theory Related Fields 117 (2000) 467-493. CrossRef
Y. Baraud, S. Huet and B. Laurent, Adaptive tests of linear hypotheses by model selection. Ann. Statist. 31 (2003).
Y. Baraud, S. Huet and B. Laurent, Tests for convex hypotheses, Technical Report 2001-66. University of Paris XI, France (2001).
Brunk, H.D., On the estimation of parameters restricted by inequalities. Ann. Math. Statist. 29 (1958) 437-454. CrossRef
Dümbgen, L. and Spokoïny, V.G., Multiscale testing of qualitative hypotheses. Ann. Statist. 29 (2001) 124-152. CrossRef
Ghosal, S., Sen, A. and van der Vaart, A., Testing monotonicity of regression. Ann. Statist. 28 (2000) 1054-1082. CrossRef
Gijbels, I., Hall, P., Jones, M.C. and Koch, I., Tests for monotonicity of a regression mean with guaranteed level. Biometrika 87 (2000) 663-673. CrossRef
Hall, P. and Heckman, N., Testing for monotonicity of a regression mean by calibrating for linear functions. Ann. Statist. 28 (2000) 20-39.
I.A. Ibragimov and R.Z. Has'minskii, Statistical estimation. Asymptotic theory. Springer-Verlag, New York-Berlin, Appl. Math. 16 (1981).
Juditsky, A. and Nemirovski, A., On nonparametric tests of positivity/monotonicity/convexity. Ann. Statist. 30 (2002) 498-527. CrossRef
Laurent, B. and Massart, P., Adaptive estimation of a quadratic functional by model selection. Ann. Statist. 28 (2000) 1302-1338.