Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Di Crescenzo, Antonio
and
Martinucci, Barbara
2007.
Computer Aided Systems Theory – EUROCAST 2007.
Vol. 4739,
Issue. ,
p.
163.
Orsingher, E.
and
De Gregorio, A.
2007.
Random Flights in Higher Spaces.
Journal of Theoretical Probability,
Vol. 20,
Issue. 4,
p.
769.
Kolesnik, Alexander D.
2008.
Random Motions at Finite Speed in Higher Dimensions.
Journal of Statistical Physics,
Vol. 131,
Issue. 6,
p.
1039.
Di Crescenzo, Antonio
and
Martinucci, Barbara
2010.
A Damped Telegraph Random Process with Logistic Stationary Distribution.
Journal of Applied Probability,
Vol. 47,
Issue. 1,
p.
84.
Di Crescenzo, Antonio
and
Martinucci, Barbara
2010.
A Damped Telegraph Random Process with Logistic Stationary Distribution.
Journal of Applied Probability,
Vol. 47,
Issue. 01,
p.
84.
Beghin, Luisa
and
Orsingher, Enzo
2010.
Poisson-Type Processes Governed by Fractional and Higher-Order Recursive Differential Equations.
Electronic Journal of Probability,
Vol. 15,
Issue. none,
Beghin, Luisa
and
Orsingher, Enzo
2010.
Moving randomly amid scattered obstacles.
Stochastics,
Vol. 82,
Issue. 2,
p.
201.
De Gregorio, Alessandro
and
Orsingher, Enzo
2012.
Flying randomly in Rd with Dirichlet displacements.
Stochastic Processes and their Applications,
Vol. 122,
Issue. 2,
p.
676.
De Gregorio, Alessandro
2012.
On Random Flights with Non-uniformly Distributed Directions.
Journal of Statistical Physics,
Vol. 147,
Issue. 2,
p.
382.
Bshouty, Daoud
Di Crescenzo, Antonio
Martinucci, Barbara
and
Zacks, Shelemyahu
2012.
Generalized Telegraph Process with Random Delays.
Journal of Applied Probability,
Vol. 49,
Issue. 03,
p.
850.
Bshouty, Daoud
Di Crescenzo, Antonio
Martinucci, Barbara
and
Zacks, Shelemyahu
2012.
Generalized Telegraph Process with Random Delays.
Journal of Applied Probability,
Vol. 49,
Issue. 3,
p.
850.
Di Crescenzo, Antonio
and
Martinucci, Barbara
2013.
On the Generalized Telegraph Process with Deterministic Jumps.
Methodology and Computing in Applied Probability,
Vol. 15,
Issue. 1,
p.
215.
Ghosh, Arka
Rastegar, Reza
and
Roitershtein, Alexander
2014.
On a directionally reinforced random walk.
Proceedings of the American Mathematical Society,
Vol. 142,
Issue. 9,
p.
3269.
2021.
Random Motions in Markov and Semi‐Markov Random Environments 2.
p.
177.
2021.
Random Motions in Markov and Semi‐Markov Random Environments 1.
p.
205.
Cinque, Fabrizio
and
Orsingher, Enzo
2023.
Stochastic Dynamics of Generalized Planar Random Motions with Orthogonal Directions.
Journal of Theoretical Probability,
Vol. 36,
Issue. 4,
p.
2229.
Cinque, Fabrizio
and
Orsingher, Enzo
2023.
Random motions in R3 with orthogonal directions.
Stochastic Processes and their Applications,
Vol. 161,
Issue. ,
p.
173.
Di Crescenzo, Antonio
Iuliano, Antonella
and
Mustaro, Verdiana
2023.
On Some Finite-Velocity Random Motions Driven by the Geometric Counting Process.
Journal of Statistical Physics,
Vol. 190,
Issue. 3,
Iuliano, Antonella
and
Verasani, Gabriella
2024.
A Cyclic Random Motion in $$\mathbb {R}^3$$ Driven by Geometric Counting Processes.
Methodology and Computing in Applied Probability,
Vol. 26,
Issue. 2,
Cinque, Fabrizio
and
Cintoli, Mattia
2024.
Multidimensional random motions with a natural number of finite velocities.
Advances in Applied Probability,
Vol. 56,
Issue. 3,
p.
1033.
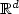 -space withn directions
-space withn directions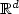 . The particle can taken possible directions with different velocities and the changes ofdirection occur at random times. The speed-vectors as well as thesupport of the distribution form a polyhedron (the first one havingconstant sides and the other expanding with time t). Thedistribution of the location of the particle is made up of twocomponents: a singular component (corresponding to the beginning ofthe travel of the particle) and an absolutely continuous component.
We completely describe the singular component and exhibit anintegral representation for the absolutely continuous one. Thedistribution is obtained by using a suitable expression of thelocation of the particle as well as some probability calculustogether with some linear algebra. The particular case of theminimal cyclic motion (n=d+1) with Erlangian switching times isalso investigated and the related distribution can be expressed interms of hyper-Bessel functions with several arguments.
. The particle can taken possible directions with different velocities and the changes ofdirection occur at random times. The speed-vectors as well as thesupport of the distribution form a polyhedron (the first one havingconstant sides and the other expanding with time t). Thedistribution of the location of the particle is made up of twocomponents: a singular component (corresponding to the beginning ofthe travel of the particle) and an absolutely continuous component.
We completely describe the singular component and exhibit anintegral representation for the absolutely continuous one. Thedistribution is obtained by using a suitable expression of thelocation of the particle as well as some probability calculustogether with some linear algebra. The particular case of theminimal cyclic motion (n=d+1) with Erlangian switching times isalso investigated and the related distribution can be expressed interms of hyper-Bessel functions with several arguments.
