Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-10T20:12:25.974Z Has data issue: false hasContentIssue false
  • English
  • Français

Functional inequalities for discrete gradients and application to the geometric distribution

Published online by Cambridge University Press:  15 September 2004

Aldéric Joulin  and
Nicolas Privault
Aldéric Joulin
Affiliation:
Laboratoire de Mathématiques, Université de La Rochelle, avenue Michel Crépeau, 17042 La Rochelle Cedex, France; nprivaul@univ-lr.fr.; ajoulin@univ-lr.fr.
Nicolas Privault
Affiliation:
Laboratoire de Mathématiques, Université de La Rochelle, avenue Michel Crépeau, 17042 La Rochelle Cedex, France; nprivaul@univ-lr.fr.; ajoulin@univ-lr.fr.
Get access

Abstract

We present several functional inequalitiesfor finite difference gradients, such asa Cheeger inequality, Poincaré and (modified) logarithmic Sobolev inequalities,associated deviation estimates,and an exponential integrability property.In the particular case of the geometric distribution on ${\mathbb{N}}$ 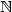we use an integration by parts formula to computethe optimal isoperimetric and Poincaré constants,and to obtain an improvement of ourgeneral logarithmic Sobolev inequality.By a limiting procedure we recover the correspondinginequalities for the exponential distribution.These results have applications to interacting spin systems undera geometric reference measure.

Keywords

Geometric distributionisoperimetrylogarithmic Sobolev inequalitiesspectral gapHerbst methoddeviation inequalitiesGibbs measures.
Type
Research Article
Information
ESAIM: Probability and Statistics , Volume 8 , August 2004 , pp. 87 - 101
Copyright
© EDP Sciences, SMAI, 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bobkov, S., Houdré, C. and Tetali, P., λ∞, vertex isoperimetry and concentration. Combinatorica 20 (2000) 153–172. CrossRef
Bobkov, S. and Ledoux, M., Poincaré's inequalities and Talagrand's concentration phenomenon for the exponential distribution. Probab. Theory Relat. Fields 107 (1997) 383–400. CrossRef
Bobkov, S.G. and Ledoux, M., On modified logarithmic Sobolev inequalities for Bernoulli and Poisson measures. J. Funct. Anal. 156 (1998) 347–365. CrossRef
Bobkov, S.G. and Götze, F., Discrete isoperimetric and Poincaré-type inequalities. Probab. Theory Relat. Fields 114 (1999) 245–277. CrossRef
Bobkov, S.G. and Houdré, C., Isoperimetric constants for product probability measures. Ann. Probab. 25 (1997) 184–205.
Cacoullos, T. and Papathanasiou, V., Characterizations of distributions by generalizations of variance bounds and simple proofs of the CLT. J. Statist. Plann. Inference 63 (1997) 157–171. CrossRef
J. Cheeger, A lower bound for the smallest eigenvalue of the Laplacian, in Problems in analysis (Papers dedicated to Salomon Bochner, 1969) Princeton Univ. Press, Princeton, N.J. (1970) 195–199.
Chen, L.H.Y. and Lou, J.H., Characterization of probability distributions by Poincaré-type inequalities. Ann. Inst. H. Poincaré Probab. Statist. 23 (1987) 91–110.
Dai Pra, P., Paganoni, A.M. and Posta, G., Entropy inequalities for unbounded spin systems. Ann. Probab. 30 (2002) 1959–1976.
Diaconis, P. and Stroock, D., Geometric bounds for eigenvalues of Markov chains. Ann. Appl. Probab. 1 (1991) 36–61. CrossRef
P. Fougères, Spectral gap for log-concave probability measures on the real line. Preprint (2002).
Gross, L., Logarithmic Sobolev inequalities. Amer. J. Math. 97 (1975) 1061–1083. CrossRef
Houdré, C., Remarks on deviation inequalities for functions of infinitely divisible random vectors. Ann. Probab. 30 (2002) 1223–1237.
Houdré, C. and Privault, N., Concentration and deviation inequalities in infinite dimensions via covariance representations. Bernoulli 8 (2002) 697–720.
C. Houdré and P. Tetali, Isoperimetric invariants for product Markov chains and graph products. Combinatorica. To appear.
M. Ledoux, Concentration of measure and logarithmic Sobolev inequalities, in Séminaire de Probabilités XXXIII, Lect. Notes Math. 1709 (1999) 120–216. CrossRef
Miclo, L., An example of application of discrete Hardy's inequalities. Markov Process. Related Fields 5 (1999) 319–330.
T. Stoyanov, Isoperimetric and related constants for graphs and Markov chains. Ph.D. Thesis, Georgia Institute of Technology (2001).