Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-28T16:25:48.447Z Has data issue: false hasContentIssue false
  • English
  • Français

Limit theorems for some functionals with heavy tails of adiscrete time Markov chain

Published online by Cambridge University Press:  08 October 2014

Patrick Cattiaux  and
Mawaki Manou-Abi
Patrick Cattiaux
Affiliation:
Institut de Mathématiques de Toulouse. CNRS UMR 5219. Université Paul Sabatier, 118 route de Narbonne, 31062 Toulouse cedex 09, France. cattiaux@math.univ-toulouse.fr; manoumawaki@gmail.com
Mawaki Manou-Abi
Affiliation:
Institut de Mathématiques de Toulouse. CNRS UMR 5219. Université Paul Sabatier, 118 route de Narbonne, 31062 Toulouse cedex 09, France. cattiaux@math.univ-toulouse.fr; manoumawaki@gmail.com
Get access

Abstract

Consider an irreducible, aperiodic and positive recurrent discrete time Markov chain(Xn,n ≥0) with invariant distribution μ. We shall investigate thelong time behaviour of some functionals of the chain, in particular the additivefunctional \hbox{$S_{n}=\sum_{i=1}^{n}f(X_{i})$}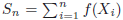Sn=∑i=1nf(Xi) for a possibly non square integrable functionf. To thisend we shall link ergodic properties of the chain to mixing properties, extending knownresults in the continuous time case. We will then use existing results of convergence tostable distributions, obtained in [M. Denker and A. Jakubowski, Stat. Probab.Lett. 8 (1989) 477–483; M. Tyran-Kaminska, StochasticProcess. Appl. 120 (2010) 1629–1650; D. Krizmanic, Ph.D. thesis(2010); B. Basrak, D. Krizmanic and J. Segers, Ann. Probab. 40(2012) 2008–2033] for stationary mixing sequences. Contrary to the usualL^2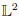L2 frameworkstudied in [P. Cattiaux, D. Chafai and A. Guillin, ALEA, Lat. Am. J. Probab. Math.Stat. 9 (2012) 337–382], where weak forms of ergodicity aresufficient to ensure the validity of the Central Limit Theorem, we will need here strongergodic properties: the existence of a spectral gap, hyperboundedness (orhypercontractivity). These properties are also discussed. Finally we give explicitexamples.

Keywords

Markov chainsstable limit theoremsstable distributionslog-Sobolev inequalityadditive functionalsfunctional limit theorem
Type
Research Article
Information
ESAIM: Probability and Statistics , Volume 18 , 2014 , pp. 468 - 482
Copyright
© EDP Sciences, SMAI 2014

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

C. Ané, S. Blachère, D. Chafaï, P. Fougères, I. Gentil, F. Malrieu, C. Roberto and G. Scheffer, Sur les inégalités de Sobolev logarithmiques. Vol. 10 of Panoramas et Synthèses. Société Mathématique de France, Paris (2000).
Bakry, D., Cattiaux, P. and Guillin, A., Rate of convergence for ergodic continuous Markov processes: Lyapunov versus Poincaré. J. Func. Anal. 254 (2008) 727–759. Google Scholar
Bartkiewicz, K., Jakubowski, A., Mikosch, T. and Wintenberger, O., Stable limits for sums of dependent infinite variance random variables. Probab. Theory Relat. Fields 150 (2011) 337–372. Google Scholar
Basrak, B., Krizmanic, D. and Segers, J., A functional limit theorem for dependent sequences with infinite variance stable limits. Ann. Probab. 40 (2012) 2008–2033. Google Scholar
Cattiaux, P., A pathwise approach of some classical inequalities. Potential Analysis 20 (2004) 361–394. Google Scholar
Cattiaux, P., Chafai, D. and Guillin, A., Central Limit Theorem for additive functionals of ergodic Markov Diffusions. ALEA, Lat. Am. J. Probab. Math. Stat. 9 (2012) 337–382. Google Scholar
Cattiaux, P. and Guillin, A., Deviation bounds for additive functionals of Markov processes. ESAIM: PS 12 (2008) 12–29. Google Scholar
Cattiaux, P. and Guillin, A., Trends to equilibrium in total variation distance. Ann. Inst. Henri Poincaré. Prob. Stat. 45 (2009) 117–145. Google Scholar
Cattiaux, P., Guillin, A. and Roberto, C., Poincaré inequality and the ?p convergence of semi-groups. Elec. Commun. Prob. 15 (2010) 270–280. Google Scholar
Cattiaux, P., Guillin, A. and Zitt, P.A., Poincaré inequalities and hitting times. Ann. Inst. Henri Poincaré. Prob. Stat. 49 (2013) 95–118. Google Scholar
Mu-Fa Chen, Eigenvalues, inequalities, and ergodic theory. Probab. Appl. (New York). Springer-Verlag London Ltd., London (2005).
Davis, R.A., Stable limits for partial sums of dependent random variables. Ann. Probab. 11 (1983) 262–269. CrossRefGoogle Scholar
Denker, M. and Jakubowski, A., Stable limit theorems for strongly mixing sequences. Stat. Probab. Lett. 8 (1989) 477–483. Google Scholar
Jakubowski, A., Minimal conditions in p-stable limit theorem. Stochastic Process. Appl. 44 (1993) 291–327. Google Scholar
Jara, M., Komorowski, T. and Olla, S., Limit theorems for additive functionals of a Markov chain. Ann. Appl. Probab. 19 (2009) 2270–2300. Google Scholar
D. Krizmanic, Functional limit theorems for weakly dependent regularly varying time series. Ph.D. thesis (2010). Available at http://www.math.uniri.hr/˜dkrizmanic/DKthesis.pdf.
S.P. Meyn and R.L. Tweedie, Markov chains and stochastic stability. Commun. Control Eng. Series. Springer-Verlag London Ltd., London (1993).
Merlevède, F., Peligrad, M. and Utev, S., Recent advances in invariance principles for stationary sequences. Probab. Surv. 3 (2006) 1–36. Google Scholar
L. Miclo, On hyperboundedness and spectrum of Markov operators. Preprint, available on hal-00777146 (2013).
Röckner, M. and Wang, F.Y., Weak Poincaré inequalities and L 2-convergence rates of Markov semi-groups. J. Funct. Anal. 185 (2001) 564–603. Google Scholar
Tyran-Kaminska, M., Convergence to Lévy stable processes under some weak dependence conditions. Stochastic Process. Appl. 120 (2010) 1629–1650. Google Scholar
Van Doorn, E. and Schrdner, P., Geometric ergodicity and quasi-stationnarity in discrete time Birth-Death processes. J. Austral. Math. Soc. Ser. B 37 (1995) 121–144. Google Scholar