Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T22:34:59.997Z Has data issue: false hasContentIssue false
  • English
  • Français

Limit theorems for U-statistics indexed by a onedimensional random walk

Published online by Cambridge University Press:  15 November 2005

Nadine Guillotin-Plantard  and
Véronique Ladret
Nadine Guillotin-Plantard
Affiliation:
Université Claude Bernard, Lyon 1, 50 av. Tony-Garnier, 69366 Lyon Cedex 07, France; nadine.guillotin@univ-lyon1.fr; veronique.ladret@univ-lyon1.fr
Véronique Ladret
Affiliation:
Université Claude Bernard, Lyon 1, 50 av. Tony-Garnier, 69366 Lyon Cedex 07, France; nadine.guillotin@univ-lyon1.fr; veronique.ladret@univ-lyon1.fr
Get access

Abstract

Let (Sn)n≥0 be a $\mathbb Z$ 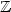-random walk and $(\xi_{x})_{x\in \mathbb Z}$ 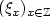be a sequence of independent andidentically distributed $\mathbb R$ 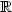-valued random variables,independent of the random walk. Let h be a measurable, symmetricfunction defined on $\mathbb R^2$ 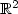with values in $\mathbb R$ 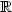. We study theweak convergence of the sequence ${\cal U}_{n}, n\in \mathbb N$ 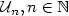, withvalues in D[0,1] the set of right continuous real-valuedfunctions with left limits, defined by \[ \sum_{i,j=0}^{[nt]}h(\xi_{S_{i}},\xi_{S_{j}}), t\in[0,1].\] 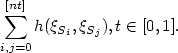Statistical applications are presented, in particular we prove a strong law of large numbersfor U-statistics indexed by a one-dimensional random walk using a result of [1].

Keywords

Random walkrandom sceneryU-statisticsfunctional limit theorem.
Type
Research Article
Information
ESAIM: Probability and Statistics , Volume 9 , February 2005 , pp. 98 - 115
Copyright
© EDP Sciences, SMAI, 2005

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aaronson, J., Burton, R., Dehling, H., Gilat, D., Hill, T. and Weiss, B., Strong laws for L- and U-statistics. Trans. Amer. Math. Soc. 348 (1996) 2845–2866. CrossRef
P. Billingsley, Convergence of probability measures. Wiley Series in Probability and Statistics: Probability and Statistics. John Wiley & Sons Inc., New York, second edition. A Wiley-Interscience Publication (1999).
Bolthausen, E., A central limit theorem for two-dimensional random walks in random sceneries. Ann. Probab. 17 (1989) 108–115. CrossRef
Boylan, E., Local times for a class of Markoff processes. Illinois J. Math. 8 (1964) 19–39.
Buffet, E. and Pulé, J.V., A model of continuous polymers with random charges. J. Math. Phys. 38 (1997) 5143–5152. CrossRef
Cabus, P. and Guillotin-Plantard, N., Functional limit theorems for U-statistics indexed by a random walk. Stochastic Process. Appl. 101 (2002) 143–160. CrossRef
den Hollander, F., Mixing properties for random walk in random scenery. Ann. Probab. 16 (1988) 1788–1802. CrossRef
den Hollander, F., Keane, M.S., Serafin, J. and Steif, J.E., Weak bernoullicity of random walk in random scenery. Japan. J. Math. (N.S.) 29 (2003) 389–406.
den Hollander, F. and Steif, J.E., Mixing properties of the generalized T,T-1 -process. J. Anal. Math. 72 (1997) 165–202. CrossRef
Getoor, R.K. and Kesten, H., Continuity of local times for Markov processes. Comp. Math. 24 (1972) 277–303.
W. Hoeffding, The strong law of large numbers for U-statistics. Univ. N. Carolina, Institue of Stat. Mimeo series 302 (1961).
Kesten, H. and Spitzer, F., A limit theorem related to a new class of self-similar processes. Z. Wahrsch. Verw. Gebiete 50 (1979) 5–25. CrossRef
A.J. Lee, U-statistics. Theory and practice. Marcel Dekker, Inc., New York (1990).
Maejima, M., Limit theorems related to a class of operator-self-similar processes. Nagoya Math. J. 142 (1996) 161–181. CrossRef
Martínez, S. and Petritis, D., Thermodynamics of a Brownian bridge polymer model in a random environment. J. Phys. A 29 (1996) 1267–1279. CrossRef
Meilijson, I., Mixing properties of a class of skew-products. Israel J. Math. 19 (1974) 266–270. CrossRef
D. Revuz and M. Yor, Continuous martingales and Brownian motion. Springer-Verlag, Berlin. Fundamental Principles of Mathematical Sciences 293 (1999).
R.J. Serfling, Approximation theorems of mathematical statistics. John Wiley & Sons Inc., New York. Wiley Series in Probability and Mathematical Statistics (1980).
F. Spitzer, Principles of random walks. Springer-Verlag, New York, second edition. Graduate Texts in Mathematics 34 (1976).