Minimax nonparametric hypothesis testingfor ellipsoids and Besov bodies

Abstract

We observe an infinitely dimensional Gaussian random vector x = ξ + vwhereξ is a sequence of standard Gaussian variables and v ∈ l₂ is anunknownmean. We consider the hypothesis testing problem H₀ : v = 0versusalternatives $H_{\varepsilon,\tau}:v\in V_{\varepsilon}$ 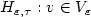for the sets $V_{\varepsilon}=V_{\varepsilon}(\tau,\rho_{\varepsilon})\subset l_2$ 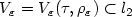.The sets V_ε are l _q -ellipsoidsof semi-axes a_i = i^-s R/ε with l _p -ellipsoidof semi-axes b_i = i^-r p^ε/ε removed orsimilar Besov bodies B^q,t;s (R/ε) with Besovbodies B^p,h;r (p^ε/ε) removed. Here $\tau =(\kappa,R)$ 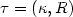or $\tau =(\kappa,h,t,R);\ \\kappa=(p,q,r,s)$ 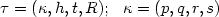are the parameters which define thesets V_ε for given radii p_ε → 0,0 < p,q,h,t ≤ ∞, -∞ ≤ r,s ≤ ∞, R > 0; ε → 0 is theasymptotical parameter.We study the asymptotics of minimaxsecond kind errors $\beta_{\varepsilon}(\alpha)=\beta(\alpha, V_{\varepsilon}(\tau,\rho_{\varepsilon}))$ 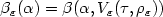and construct asymptotically minimax or minimax consistent families oftests $\psi_{\alpha;\varepsilon,\tau,\rho_{\varepsilon}}$ 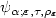, if it is possible.We describe the partition of the set of parameters κ into regions withdifferent types of asymptotics: classical, trivial, degenerate and Gaussian(of various types).Analogous rates have been obtained in a signal detectionproblem for continuous variant of white noise model: alternativescorrespond to Besov or Sobolev balls with Besov or Sobolev balls removed.The study is based on an extension of methods of constructions ofasymptotically least favorable priors.These methods are applicable to wide class of “convex separablesymmetrical" infinite-dimensional hypothesis testingproblems in white Gaussian noise model. Under some assumptionsthese methodsare based on the reduction of hypothesis testing problemto convex extreme problem: to minimize specially defined Hilbert normover convex sets of sequences $\bar{\pi}$ 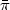of measures π_i on thereal line. The study of this extreme problem allows to obtain differenttypes of Gaussian asymptotics.If necessary assumptions do not hold, then we obtain other types ofasymptotics.