Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-28T16:00:31.791Z Has data issue: false hasContentIssue false
  • English
  • Français

Model selection for regression on a random design

Published online by Cambridge University Press:  15 November 2002

Yannick Baraud
Yannick Baraud*
Affiliation:
École Normale Supérieure, DMA, 45 rue d'Ulm, 75230 Paris Cedex 05, France; yannick.baraud@ens.fr.
Get access

Abstract

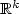We consider the problem of estimating an unknown regression function when the design is random with values in $\mathbb{R}^k$. Our estimation procedure is based on model selection and does not rely on any prior information on the target function. We start with a collection of linear functional spaces and build, on a data selected space among this collection, the least-squares estimator. We study the performance of an estimator which is obtained by modifying this least-squares estimator on a set of small probability. For the so-defined estimator, we establish nonasymptotic risk bounds that can be related to oracle inequalities. As a consequence of these, we show that our estimator possesses adaptive properties in the minimax sense over large families of Besov balls Bα,l,∞(R) with R>0, l ≥ 1 and α > α1 where α1 is a positive number satisfying 1/l - 1/2 ≤ α1 < 1/l. We also study the particular case where the regression function is additive and then obtain an additive estimator which converges at the same rate as it does when k=1.


Keywords

Nonparametric regressionleast-squares estimatorspenalized criteriaminimax ratesBesov spacesmodel selectionadaptive estimation.
Type
Research Article
Information
ESAIM: Probability and Statistics , Volume 6: New directions in Time Series Analysis (Guest Editor: Philippe Soulier)New directions in Time Series Analysis (Guest Editor: Philippe Soulier) , 2002 , pp. 127 - 146
Copyright
© EDP Sciences, SMAI, 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baraud, Y., Model selection for regression on a fixed design. Probab. Theory Related Fields 117 (2000) 467-493. CrossRef
Barron, A., Birgé, L. and Massart, P., Risk bounds for model selection via penalization. Probab. Theory Related Fields 113 (1999) 301-413. CrossRef
Barron, A.R. and Cover, T.M., Minimum complexity density estimation. IEEE Trans. Inform. Theory 37 (1991) 1738. CrossRef
Birgé, L. and Massart, P., An adaptive compression algorithm in Besov spaces. Constr. Approx. 16 (2000) 1-36. CrossRef
Birgé, L. and Massart, P., Minimum contrast estimators on sieves: Exponential bounds and rates of convergence. Bernoulli 4 (1998) 329-375. CrossRef
Birgé, L. and Massart, P., Gaussian model selection. JEMS 3 (2001) 203-268.
L. Birgé and Massart, A generalized C p criterion for Gaussian model selection, Technical Report. University Paris 6, PMA-647 (2001).
L. Birgé and Y. Rozenholc, How many bins should be put in a regular histogram, Technical Report. University Paris 6, PMA-721 (2002).
O. Catoni, Statistical learning theory and stochastic optimization, in École d'été de probabilités de Saint-Flour. Springer (2001).
Cohen, A., Daubechies, I. and Vial, P., Wavelet and fast wavelet transform on an interval. Appl. Comp. Harmon. Anal. 1 (1993) 54-81. CrossRef
I. Daubechies, Ten lectures on wavelets. SIAM: Philadelphia (1992).
R.A. DeVore and G.G. Lorentz, Constructive approximation. Springer-Verlag, Berlin (1993).
Donoho, D.L. and Johnstone, I.M., Ideal spatial adaptation via wavelet shrinkage. Biometrika 81 (1994) 425-455. CrossRef
Donoho, D.L. and Johnstone, I.M., Minimax estimation via wavelet shrinkage. Ann. Statist. 26 (1998) 879-921.
Kohler, M., Inequalities for uniform deviations of averages from expectations with applications to nonparametric regression. J. Statist. Plann. Inference 89 (2000) 1-23. CrossRef
Kohler, M., Nonparametric regression function estimation using interaction least square splines and complexity regularization. Metrika 47 (1998) 147-163. CrossRef
A.P. Korostelev and A.B. Tsybakov, Minimax theory of image reconstruction. Springer-Verlag, New York NY, Lecture Notes in Statis. (1993).
Stone, C.J., Additive regression and other nonparametric models. Ann. Statist. 13 (1985) 689-705. CrossRef
M. Wegkamp, Model selection in non-parametric regression, Preprint. Yale University (2000).
Yang, Y., Model selection for nonparametric regression. Statist. Sinica 9 (1999) 475-499.
Yang, Y., Combining different procedures for adaptive regression. J. Multivariate Anal. 74 (2000) 135-161. CrossRef
Yang, Y. and Barron, A., Information-Theoretic determination of minimax rates of convergence. Ann. Statist. 27 (1999) 1564-1599.