Article contents
Penultimate approximation for the distribution of the excesses
Published online by Cambridge University Press: 15 November 2002
Abstract
Let F be a distribution function (d.f) in the domain of attraction of an extreme value distribution ${ H_{\gamma} }$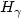 ; it is well-known that Fu(x), where Fu is the d.f of the excesses over u, converges, when u tends to s+(F), the end-point of F, to $G_{\gamma}(\frac{x}{\sigma(u)})$
; it is well-known that Fu(x), where Fu is the d.f of the excesses over u, converges, when u tends to s+(F), the end-point of F, to $G_{\gamma}(\frac{x}{\sigma(u)})$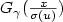 , where $G_{\gamma}$
, where $G_{\gamma}$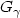 is the d.f. of the Generalized Pareto Distribution. We provide conditions that ensure that there exists, for $\gamma >-1$
is the d.f. of the Generalized Pareto Distribution. We provide conditions that ensure that there exists, for $\gamma >-1$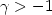 , a function Λ which verifies $\lim_{u \rightarrow s_+(F)} \Lambda (u) =\gamma$
, a function Λ which verifies $\lim_{u \rightarrow s_+(F)} \Lambda (u) =\gamma$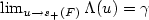 and is such that $\Delta(u)= \sup_{x \in[0,s_+(F)-u[} |\bar{F}_u(x) - \bar{G}_{\Lambda(u)} (x/ \sigma(u))| $
and is such that $\Delta(u)= \sup_{x \in[0,s_+(F)-u[} |\bar{F}_u(x) - \bar{G}_{\Lambda(u)} (x/ \sigma(u))| $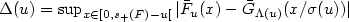 converges to 0 faster than $d(u)=\sup_{x \in[0,s_+(F)-u[} |\bar{F}_u(x) - \bar{G}_{\gamma}(x/ \sigma(u))|$
converges to 0 faster than $d(u)=\sup_{x \in[0,s_+(F)-u[} |\bar{F}_u(x) - \bar{G}_{\gamma}(x/ \sigma(u))|$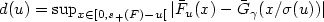 .
.
Information
- Type
- Research Article
- Information
- Copyright
- © EDP Sciences, SMAI, 2002
References
- 7
- Cited by

