Article contents
Convergence to a self-similar solution for a one-phase Stefan problem arising in corrosion theory
Published online by Cambridge University Press: 09 August 2022
Abstract
Steel corrosion plays a central role in different technological fields. In this article, we consider a simple case of a corrosion phenomenon which describes a pure iron dissolution in sodium chloride. This article is devoted to prove rigorously that under rather general hypotheses on the initial data, the solution of this iron dissolution model converges to a self-similar profile as 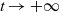 $t\rightarrow +\infty$. We will do so for an equivalent formulation as presented in the book of Avner Friedman about parabolic equations (Friedman (1964) Partial Differential Equations of Parabolic Type, Prentice-Hall, Inc., Englewood Cliffs, NJ.). In order to prove the convergence result, we apply a comparison principle together with suitable upper and lower solutions.
$t\rightarrow +\infty$. We will do so for an equivalent formulation as presented in the book of Avner Friedman about parabolic equations (Friedman (1964) Partial Differential Equations of Parabolic Type, Prentice-Hall, Inc., Englewood Cliffs, NJ.). In order to prove the convergence result, we apply a comparison principle together with suitable upper and lower solutions.
Keywords
MSC classification
Information
- Type
- Papers
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
- 1
- Cited by


