Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Li, Huicong
and
Peng, Rui
2019.
Dynamics and asymptotic profiles of endemic equilibrium for SIS epidemic patch models.
Journal of Mathematical Biology,
Vol. 79,
Issue. 4,
p.
1279.
Zhang, Jialiang
and
Cui, Renhao
2020.
Asymptotic behavior of an SIS reaction–diffusion–advection model with saturation and spontaneous infection mechanism.
Zeitschrift für angewandte Mathematik und Physik,
Vol. 71,
Issue. 5,
Sun, Xueying
and
Cui, Renhao
2020.
Analysis on a diffusive SIS epidemic model with saturated incidence rate and linear source in a heterogeneous environment.
Journal of Mathematical Analysis and Applications,
Vol. 490,
Issue. 1,
p.
124212.
Han, Shuyu
Lei, Chengxia
and
Zhang, Xiaoyan
2020.
Qualitative analysis on a diffusive SIRS epidemic model with standard incidence infection mechanism.
Zeitschrift für angewandte Mathematik und Physik,
Vol. 71,
Issue. 6,
Peng, Rui
and
Wu, Yixiang
2021.
Global $L^\infty$-bounds and Long-time Behavior of a Diffusive Epidemic System in A Heterogeneous Environment.
SIAM Journal on Mathematical Analysis,
Vol. 53,
Issue. 3,
p.
2776.
Liu, Chuanxin
and
Cui, Renhao
2021.
Qualitative analysis on an SIRS reaction–diffusion epidemic model with saturation infection mechanism.
Nonlinear Analysis: Real World Applications,
Vol. 62,
Issue. ,
p.
103364.
Zhang, Jialiang
and
Cui, Renhao
2021.
Asymptotic profiles of the endemic equilibrium of a diffusive SIS epidemic system with saturated incidence rate and spontaneous infection.
Mathematical Methods in the Applied Sciences,
Vol. 44,
Issue. 1,
p.
517.
Cui, Renhao
2021.
Asymptotic profiles of the endemic equilibrium of a reaction-diffusion-advection SIS epidemic model with saturated incidence rate.
Discrete & Continuous Dynamical Systems - B,
Vol. 26,
Issue. 6,
p.
2997.
Cui, Renhao
Li, Huicong
Peng, Rui
and
Zhou, Maolin
2021.
Concentration behavior of endemic equilibrium for a reaction–diffusion–advection SIS epidemic model with mass action infection mechanism.
Calculus of Variations and Partial Differential Equations,
Vol. 60,
Issue. 5,
Ge, Jing
Lin, Zhigui
and
Zhu, Huaiping
2021.
MODELING THE SPREAD OF WEST NILE VIRUS IN A SPATIALLY HETEROGENEOUS AND ADVECTIVE ENVIRONMENT.
Journal of Applied Analysis & Computation,
Vol. 11,
Issue. 4,
p.
1868.
Inoue, Jumpei
and
Kuto, Kousuke
2021.
Impact of Regional Difference in Recovery Rate on the Total Population of Infected for a Diffusive SIS Model.
Mathematics,
Vol. 9,
Issue. 8,
p.
888.
Lei, Chengxia
Shen, Yi
Zhang, Guanghui
and
Zhang, Yuxiang
2021.
Analysis on a diffusive SEI epidemic model with/without immigration of infected hosts.
Discrete & Continuous Dynamical Systems - S,
Vol. 14,
Issue. 12,
p.
4259.
Lei, Chengxia
and
Zhou, Xinhui
2022.
Concentration phenomenon of the endemic equilibrium of a reaction-diffusion-advection SIS epidemic model with spontaneous infection.
Discrete and Continuous Dynamical Systems - B,
Vol. 27,
Issue. 6,
p.
3077.
Dong, Lingmin
Hou, Shuai
and
Lei, Chengxia
2022.
Global attractivity of the equilibria of the diffusive SIR and SEIR epidemic models with multiple parallel infectious stages and nonlinear incidence mechanism.
Applied Mathematics Letters,
Vol. 134,
Issue. ,
p.
108352.
Tian, Xuan
Guo, Shangjiang
and
Liu, Zhisu
2022.
Qualitative analysis of a diffusive SEIR epidemic model with linear external source and asymptomatic infection in heterogeneous environment.
Discrete and Continuous Dynamical Systems - B,
Vol. 27,
Issue. 6,
p.
3053.
Chen, Xiaodan
and
Cui, Renhao
2022.
Qualitative analysis on a spatial SIS epidemic model with linear source in advective environments: I standard incidence.
Zeitschrift für angewandte Mathematik und Physik,
Vol. 73,
Issue. 4,
Dong, Lingmin
Li, Bo
and
Zhang, Guanghui
2022.
Analysis on a Diffusive SI Epidemic Model with Logistic Source and Saturation Infection Mechanism.
Bulletin of the Malaysian Mathematical Sciences Society,
Vol. 45,
Issue. 3,
p.
1111.
Wei, Dan
and
Guo, Shangjiang
2022.
Hopf bifurcation of a diffusive SIS epidemic system with delay in heterogeneous environment.
Applicable Analysis,
Vol. 101,
Issue. 16,
p.
5906.
Xu, Shenghu
and
Li, Xiaojuan
2022.
Global behavior of solutions to an SI epidemic model with nonlinear diffusion in heterogeneous environment.
AIMS Mathematics,
Vol. 7,
Issue. 4,
p.
6779.
Li, Guanlin
and
Yao, Yao
2022.
Two-species competition model with chemotaxis: well-posedness, stability and dynamics.
Nonlinearity,
Vol. 35,
Issue. 3,
p.
1329.
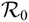 $\mathcal {R}_0$ – i.e. the unique disease-free equilibrium is globally stable if
$\mathcal {R}_0$ – i.e. the unique disease-free equilibrium is globally stable if 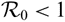 $\mathcal {R}_0\lt1$, while if
$\mathcal {R}_0\lt1$, while if 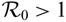 $\mathcal {R}_0\gt1$, the disease is uniformly persistent and there is an endemic equilibrium (EE), which is globally stable in some special cases with weak chemotactic sensitivity. Our results on the asymptotic profiles of EE illustrate that restricting the motility of susceptible population may eliminate the infectious disease entirely for the first model with constant total population but fails for the second model with varying total population. In particular, this implies that such cross-diffusion does not contribute to the elimination of the infectious disease modelled by the second one.
$\mathcal {R}_0\gt1$, the disease is uniformly persistent and there is an endemic equilibrium (EE), which is globally stable in some special cases with weak chemotactic sensitivity. Our results on the asymptotic profiles of EE illustrate that restricting the motility of susceptible population may eliminate the infectious disease entirely for the first model with constant total population but fails for the second model with varying total population. In particular, this implies that such cross-diffusion does not contribute to the elimination of the infectious disease modelled by the second one.
