Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-10T12:58:12.707Z Has data issue: false hasContentIssue false
  • English
  • Français

Expansions for the linear-elastic contribution to the self-interaction force of dislocation curves

Part of: Dynamical problems Plastic materials, materials of stress-rate and internal-variable type

Published online by Cambridge University Press:  20 October 2021

PATRICK VAN MEURS Open the ORCID record for PATRICK VAN MEURS [Opens in a new window]
PATRICK VAN MEURS*
Affiliation:
Faculty of Mathematics and Physics, Kanazawa University, Kanazawa, Japan email: pjpvmeurs@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

The self-interaction force of dislocation curves in metals depends on the local arrangement of the atoms and on the non-local interaction between dislocation curve segments. While these non-local segment–segment interactions can be accurately described by linear elasticity when the segments are further apart than the atomic scale of size $\varepsilon$ , this model breaks down and blows up when the segments are 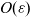$O(\varepsilon)$ apart. To separate the non-local interactions from the local contribution, various models depending on $\varepsilon$ have been constructed to account for the non-local term. However, there are no quantitative comparisons available between these models. This paper makes such comparisons possible by expanding the self-interaction force in these models in $\varepsilon$ beyond the O(1)-term. Our derivation of these expansions relies on asymptotic analysis. The practical use of these expansions is demonstrated by developing numerical schemes for them, and by – for the first time – bounding the corresponding discretisation error.

Keywords

dislocation curvesasymptotic expansiondiscretisation error

MSC classification

Primary: 74H10: Analytic approximation of solutions (perturbation methods, asymptotic methods, series, etc.)
Secondary: 74C10: Small-strain, rate-dependent theories (including theories of viscoplasticity)
Type
Papers
Information
European Journal of Applied Mathematics , Volume 33 , Issue 6 , December 2022 , pp. 1032 - 1061
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arsenlis, A., Cai, W., Tang, M., Rhee, M., Oppelstrup, T., Hommes, G., Pierce, T. G. & Bulatov, V. V. (2007). Enabling strain hardening simulations with dislocation dynamics. Model. Simul. Mater. Sci. Eng. 15(6), 553.CrossRefGoogle Scholar
Abramowitz, M. & Stegun, I. A. (1964). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, Vol. 55. US Government Printing Office.Google Scholar
Cai, W., Arsenlis, A., Weinberger, C. R. & Bulatov, V.V. (2006). A non-singular continuum theory of dislocations. J. Mech. Phys. Solids 54(3), 561–587.CrossRefGoogle Scholar
Clouet, E. (2011). Dislocation core field. I. Modeling in anisotropic linear elasticity theory. Phys. Rev. B 84(22), 224111.CrossRefGoogle Scholar
do Carmo, M. P. (2016). Differential Geometry of Curves and Surfaces: Revised and Updated, 2nd ed. Courier Dover Publications.Google Scholar
de Wit’, R. (1960). The continuum theory of stationary dislocations. In: Solid State Physics, Vol. 10. Elsevier, pp. 249–292.Google Scholar
Gavazza, S. D. & Barnett, D. M. (1976). The self-force on a planar dislocation loop in an anisotropic linear-elastic medium. J. Mech. Phys. Solids 24(4), 171–185.CrossRefGoogle Scholar
Gehlen, P. C., Hirth, J. P., Hoagland, R. G. & Kanninen, M. F. (1972). A new representation of the strain field associated with the cube-edge dislocation in a model of a $\alpha$ -iron. J. Appl. Phys. 43(10), 3921–3933.Google Scholar
Gradshteyn, I. S. & Ryzhik, I. M. (2007). Table of Integrals, Series, and Products, Seventh Edition. Burlington, Massachusetts: Academic Press.Google Scholar
Ghoniem, N. M., Tong, S.-H. & Sun, L. Z. (2000). Parametric dislocation dynamics: a thermodynamics-based approach to investigations of mesoscopic plastic deformation. Phys. Rev. B 61(2), 913.CrossRefGoogle Scholar
Hull, D. & Bacon, D. J. (2011). Introduction to Dislocations, Vol. 37. Oxford: Elsevier.Google Scholar
Henager, C. & Hoagland, R. (2005). Dislocation and stacking fault core fields in FCC metals. Philos. Mag. 85(36), 4477–4508.Google Scholar
Hirth, J. P. & Lothe, J. (1982). Theory of Dislocations. New York: John Wiley & Sons, 1982.Google Scholar
Kolář, M., Beneš, M., Kratochvl, J. & Pauš, P. (2018). Modeling of double cross-slip by means of geodesic curvature driven flow. Acta Phys. Pol. A 134(3), 667–670.CrossRefGoogle Scholar
Kundin, J., Emmerich, H. & Zimmer, J. (2011). Mathematical concepts for the micromechanical modelling of dislocation dynamics with a phase-field approach. Philos. Mag. 91(1), 97–121.CrossRefGoogle Scholar
Lesar, R. & Capolungo, L. (2020). Advances in discrete dislocation dynamics simulations. In: Handbook of Materials Modeling: Methods: Theory and Modeling, pp. 1079–1110.CrossRefGoogle Scholar
Lesar, R. (2004). Ambiguities in the calculation of dislocation self energies. Phys. Stat. Sol. (B) 241(13), 2875–2880.Google Scholar
Lothe, J. (1992). Dislocations in continuous elastic media. In: Modern Problems in Condensed Matter Sciences, Vol. 31. Elsevier, pp. 175–235.Google Scholar
Peach, M. & Koehler, J. S. (1950). The forces exerted on dislocations and the stress fields produced by them. Phys. Rev. 80(3), 436–439.CrossRefGoogle Scholar
Schwarz, K. W. (1999). Simulation of dislocations on the mesoscopic scale. I. Methods and examples. J. Appl. Phys. 85(1), 108–119.CrossRefGoogle Scholar
Zhu, Y., Chapman, S. J. & Acharya, A. (2013). Dislocation motion and instability. J. Mech. Phys. Sol. 61(8), 1835–1853.CrossRefGoogle Scholar
Zbib, H. M., Rhee, M. & Hirth, J. P. (1998). On plastic deformation and the dynamics of 3D dislocations. Int. J. Mech. Sci. 40(2–3), 113–127.CrossRefGoogle Scholar
Zhao, D., Wang, H. & Xiang, Y. (2012). Asymptotic behaviors of the stress fields in the vicinity of dislocations and dislocation segments. Philos. Mag. 92(18), 2351–2374.CrossRefGoogle Scholar