Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T06:48:13.279Z Has data issue: false hasContentIssue false
  • English
  • Français

Explicit characterization of the polarization tensor for rough thin layers

Published online by Cambridge University Press:  22 December 2010

C. POIGNARD
C. POIGNARD*
Affiliation:
INRIA Bordeaux-Sud-Ouest, Institut de Mathématiques de Bordeaux, CNRS UMR 5251 & Université de Bordeaux1, 351 cours de la Libération, F - 33405 Talence Cedex, France email: clair.poignard@inria.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

In the paper ‘Approximate transmission conditions through a rough thin layer. The case of periodic roughness’ (Eur. J. Appl. Math. 2010; 21: 51–75), Ciuperca et al. derive transmission conditions that are equivalent to a rough thin layer for the conductivity problem. These conditions involved a pair of vector fields (A0, a0) and two constants D1 and D2 that are given implicitly by solving a partial differential equation in the infinite strip 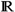× 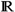/2π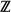. We give here an explicit expression of a0 in terms of A0, which shows that D1 equals zero. We infer an explicit characterization of the polarization tensor as given by Capdeboscq and Vogelius (ESAIM:M2AN. 2003; 37: 159–173).

Type
Papers
Information
European Journal of Applied Mathematics , Volume 22 , Issue 1 , February 2011 , pp. 1 - 6
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Capdeboscq, Y. & Vogelius, M. S. (2003) A general representation formula for boundary voltage perturbations caused by internal conductivity inhomogeneities of low volume fraction. M2AN Math. Model. Numer. Anal. 37 (1), 159–173.CrossRefGoogle Scholar
[2]Ciuperca, I.S., Jai, M. & Poignard, C. (2010) Approximate transmission conditions through a rough thin layer. The case of periodic roughness. Eur. J. App. Math. 21, 51–75.CrossRefGoogle Scholar
[3]Ciuperca, I.S., Perrussel, R. & Poignard, C. Two-scale analysis for very rough thin layers. An explicit characterization of the polarization tensor. Research Report INRIA RR-6975. http://hal.inria.fr/inria-00401835/fr/. (In press: JMPA)Google Scholar
[4]Poignard, C. (2009) Approximate transmission conditions through a weakly oscillating thin layer. Math. Methods. Appl. Sci. 32 435–453.CrossRefGoogle Scholar