Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Feng, Zhigang
2008.
Variation and Minkowski dimension of fractal interpolation surface.
Journal of Mathematical Analysis and Applications,
Vol. 345,
Issue. 1,
p.
322.
Wang, Hong-Yong
Yang, Shou-Zhi
and
Li, Xiu-Juan
2008.
Error analysis for bivariate fractal interpolation functions generated by 3-D perturbed iterated function systems.
Computers & Mathematics with Applications,
Vol. 56,
Issue. 7,
p.
1684.
METZLER, WOLFGANG
and
YUN, CHOL HUI
2010.
CONSTRUCTION OF FRACTAL INTERPOLATION SURFACES ON RECTANGULAR GRIDS.
International Journal of Bifurcation and Chaos,
Vol. 20,
Issue. 12,
p.
4079.
Bouboulis, P.
2010.
Construction of Fractal Surfaces via Solutions of Partial Differential Equations.
SRX Mathematics,
Vol. 2010,
Issue. ,
p.
1.
Bouboulis, P.
and
Mavroforakis, M.
2011.
Reproducing Kernel Hilbert Spaces and fractal interpolation.
Journal of Computational and Applied Mathematics,
Vol. 235,
Issue. 12,
p.
3425.
CHAND, A. K. B.
2012.
NATURAL CUBIC SPLINE COALESCENCE HIDDEN VARIABLE FRACTAL INTERPOLATION SURFACES.
Fractals,
Vol. 20,
Issue. 02,
p.
117.
WANG, HONG-YONG
and
JI, JIA-BING
2012.
SURFACE FITTING AND ERROR ANALYSIS USING FRACTAL INTERPOLATION.
International Journal of Bifurcation and Chaos,
Vol. 22,
Issue. 08,
p.
1250194.
Wang, Hong-Yong
and
Yu, Jia-Shan
2013.
Fractal interpolation functions with variable parameters and their analytical properties.
Journal of Approximation Theory,
Vol. 175,
Issue. ,
p.
1.
Ji, Jiabing
and
Peng, Jigen
2013.
Analytical properties of bivariate fractal interpolation functions with vertical scaling factor functions.
International Journal of Computer Mathematics,
Vol. 90,
Issue. 3,
p.
539.
Yun, Chol-hui
O, Hyong-chol
and
Choi, Hui-chol
2014.
Construction of fractal surfaces by recurrent fractal interpolation curves.
Chaos, Solitons & Fractals,
Vol. 66,
Issue. ,
p.
136.
CHAND, A. K. B.
VISWANATHAN, P.
and
REDDY, K. M.
2015.
TOWARDS A MORE GENERAL TYPE OF UNIVARIATE CONSTRAINED INTERPOLATION WITH FRACTAL SPLINES.
Fractals,
Vol. 23,
Issue. 04,
p.
1550040.
YUN, CHOL-HUI
CHOI, HUI-CHOL
and
O, HYONG-CHOL
2015.
CONSTRUCTION OF RECURRENT FRACTAL INTERPOLATION SURFACES WITH FUNCTION SCALING FACTORS AND ESTIMATION OF BOX-COUNTING DIMENSION ON RECTANGULAR GRIDS.
Fractals,
Vol. 23,
Issue. 04,
p.
1550030.
RUAN, HUO-JUN
and
XU, QIANG
2015.
FRACTAL INTERPOLATION SURFACES ON RECTANGULAR GRIDS.
Bulletin of the Australian Mathematical Society,
Vol. 91,
Issue. 3,
p.
435.
2016.
Fractal Functions, Fractal Surfaces, and Wavelets.
p.
387.
Massopust, Peter R.
2016.
Fractal Functions, Fractal Surfaces, and Wavelets.
p.
329.
Jiang, Ping
Liu, Feng
Wang, Jianzhou
and
Song, Yiliao
2016.
Cuckoo search-designated fractal interpolation functions with winner combination for estimating missing values in time series.
Applied Mathematical Modelling,
Vol. 40,
Issue. 23-24,
p.
9692.
Chand, A. K. B.
Vijender, N.
and
Navascués, M. A.
2017.
Convexity/Concavity and Stability Aspects of Rational Cubic Fractal Interpolation Surfaces.
Computational Mathematics and Modeling,
Vol. 28,
Issue. 3,
p.
407.
Nallapu, Vijender
2018.
Positivity and Stability of Rational Cubic Fractal Interpolation Surfaces.
Mediterranean Journal of Mathematics,
Vol. 15,
Issue. 3,
Liu, Tiantian
Zhang, Yunfeng
Wang, Ping
Du, Hongwei
Bao, Fangxun
and
Zhang, Caiming
2018.
Rational fractal surface interpolating scheme with variable parameters.
Computer Aided Geometric Design,
Vol. 64,
Issue. ,
p.
50.
Vijender, N.
2018.
Fractal Perturbation of Shaped Functions: Convergence Independent of Scaling.
Mediterranean Journal of Mathematics,
Vol. 15,
Issue. 6,

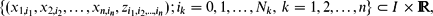
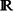 , which interpolate the data. We show that the proposed constructions generalise the previously existed ones on
, which interpolate the data. We show that the proposed constructions generalise the previously existed ones on 