Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-10T14:28:24.066Z Has data issue: false hasContentIssue false
  • English
  • Français

Global and exponential attractor of the repulsive Keller–Segel model with logarithmic sensitivity

Part of: Physiological, cellular and medical topics Parabolic equations and systems Partial differential equations

Published online by Cambridge University Press:  30 June 2020

LIN CHEN ,
FANZE KONG  and
QI WANG Open the ORCID record for QI WANG [Opens in a new window]
LIN CHEN
Affiliation:
Department of Mathematics, Southwestern University of Finance and Economics, 555 Liutai Ave, Wenjiang, Chengdu, Sichuan611130, China, emails: lchen@smail.swufe.edu.cn; fzkong@smail.swufe.edu.cn; qwang@swufe.edu.cn
FANZE KONG
Affiliation:
Department of Mathematics, Southwestern University of Finance and Economics, 555 Liutai Ave, Wenjiang, Chengdu, Sichuan611130, China, emails: lchen@smail.swufe.edu.cn; fzkong@smail.swufe.edu.cn; qwang@swufe.edu.cn
QI WANG
Affiliation:
Department of Mathematics, Southwestern University of Finance and Economics, 555 Liutai Ave, Wenjiang, Chengdu, Sichuan611130, China, emails: lchen@smail.swufe.edu.cn; fzkong@smail.swufe.edu.cn; qwang@swufe.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a Keller–Segel model that describes the cellular chemotactic movement away from repulsive chemical subject to logarithmic sensitivity function over a confined region in 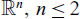${{\mathbb{R}}^n},\,n \le 2$ . This sensitivity function describes the empirically tested Weber–Fecher’s law of living organism’s perception of a physical stimulus. We prove that, regardless of chemotaxis strength and initial data, this repulsive system is globally well-posed and the constant solution is the global and exponential in time attractor. Our results confirm the ‘folklore’ that chemorepulsion inhibits the formation of non-trivial steady states within the logarithmic chemotaxis model, hence preventing cellular aggregation therein.

Keywords

Global existencechemorepulsionKeller–Segellogarithmic sensitivityexponential decay

MSC classification

Primary: 35B35: Stability
Secondary: 35K51: Initial-boundary value problems for second-order parabolic systems 35K57: Reaction-diffusion equations 92C17: Cell movement (chemotaxis, etc.)
Type
Papers
Information
European Journal of Applied Mathematics , Volume 32 , Issue 4 , August 2021 , pp. 599 - 617
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adler, J. (1966) Chemotaxis in bacteria. Science 153, 708–716.CrossRefGoogle Scholar
Adler, J. & Dahl, M. (1967) A method for measuring the motility of bacteria and for comparing random and non-random motility. J. Gen. Microbiol. 46, 161–173.CrossRefGoogle ScholarPubMed
Amann, H. (1993) Nonhomogeneous linear and quasilinear elliptic and parabolic boundary value problems. In: Function Spaces, Differential Operators and Nonlinear Analysis, Teubner, Stuttgart, Leipzig, Vol. 133, pp. 9–126.CrossRefGoogle Scholar
Biler, P., Hebisch, W. & Nadzieja, T. (1994) The Debye system: existence and large time behavior of solutions. Nonlinear Anal. 23, 1189–1209.CrossRefGoogle Scholar
Brown, D. A. & Berg, H. C. (1974) Temporal stimulation of chemotaxis in Escherichia coli. Proc. Natl. Acad. Sci. 71, 1388–1392.Google Scholar
Carrillo, J. A., Jüngel, A., Markowich, P., Toscani, G. & Unterreiter, A. (2001) Entropy dissipation methods for degenerate parabolic problems and generalized Sobolev inequalities. Monatsh. Math. 133, 1–82.CrossRefGoogle Scholar
Chen, X., Hao, J., Wang, X., Wu, Y. & Zhang, Y. (2014) Stability of spiky solution of Keller–Segel’s minimal chemotaxis model. J. Differ. Equ. 257, 3102–3134.CrossRefGoogle Scholar
Chertock, A., Kurganov, A., Wang, X. & Wu, Y. (2012) On a chemotaxis model with saturated chemotactic flux. Kinet. Relat. Models 5, 51–95.CrossRefGoogle Scholar
Childress, S. & Percus, J. (1981) Nonlinear aspects of chemotaxis. Math. Biosci. 56, 217–237.CrossRefGoogle Scholar
Crandall, M. & Rabinowitz, P. (1971) Bifurcation from simple eigenvalues, J. Funct. Anal. 8, 321–340.CrossRefGoogle Scholar
Dahlquist, F. W., Lovely, P. & Koshland Jun, D. E. (1972) Quantitative analysis of bacterial migration in chemotaxis. Nat. New Biol. 236, 120–123.CrossRefGoogle ScholarPubMed
del Pino, M., Felmer, P. & Wei, J. (1999) On the role of mean curvature in some singularly perturbed Neumann problems. SIAM J. Math. Anal. 31, 63–79.CrossRefGoogle Scholar
del Pino, M., Mahmoudi, F. & Musso, M. (2014) Bubbling on boundary submanifolds for the Lin-Ni-Takagi problem at higher critical exponents. J. Eur. Math. Soc. 16, 1687–1748.CrossRefGoogle Scholar
Engelmann, T. (1882) Über Sauerstoffausscheidung von Pflanzenzellen im Mikrospectrum. Bot. Zeit. 40, 419–426.Google Scholar
Fujie, K. (2015) Boundedness in a fully parabolic chemotaxis system with singular sensitivity. J. Math. Anal. Appl. 424, 675–684.CrossRefGoogle Scholar
Fujie, K. & Senba, T. (2018) A sufficient condition of sensitivity functions for boundedness of solutions to a parabolic-parabolic chemotaxis system. Nonlinearity 31, 1639–1672.CrossRefGoogle Scholar
Gu, Y., Wang, Q. & Yi, G. (2017) Stationary patterns and their selection mechanism of urban crime models with heterogeneous near-repeat victimization effect. European J. Appl. Math. 28, 141–178.CrossRefGoogle Scholar
Gui, C. & Wei, J. (1999) Multiple interior peak solutions for some singularly perturbed Neumann problems. J. Differ. Equ. 158, 1–27.CrossRefGoogle Scholar
Herrero, M. A. & Velázquez, J. J. L. (1996) Chemotactic collapse for the Keller–Segel model. J. Math. Biol. 35, 177–194.CrossRefGoogle ScholarPubMed
Hillen, T. & Painter, K. J. (2009) A user’s guide to PDE models for chemotaxis. J. Math. Biol. 58, 183–217.CrossRefGoogle ScholarPubMed
Horstmann, D. & Winkler, M. (2005) Boundedness vs. blow-up in a chemotaxis system. J. Differ. Equ. 215, 52–107.CrossRefGoogle Scholar
Ishida, S., Seki, K. & Yokota, T. (2014) Boundedness in quasilinear Kellel–Segel systems of parabolic-parabolic type on non-convex bounded domains. J. Differ. Equ. 256, 2993–3010.CrossRefGoogle Scholar
Kalinin, Y.V., Jiang, L., Tu, Y. & Wu, M. (2009) Logarithmic sensing in Escherichia coli bacterial chemotaxis. Biophys. J. 96, 2439–2448.CrossRefGoogle ScholarPubMed
Keller, E. & Segel, L. (1970) Initiation of slime mold aggregation viewed as an instability. J. Theor. Biol. 26, 399–415.CrossRefGoogle ScholarPubMed
Keller, E. & Segel, L. (1971) Model for chemotaxis. J. Theor. Biol. 30, 225–234.CrossRefGoogle ScholarPubMed
Keller, E. & Segel, L. (1971) Traveling bands of chemotactic bacteria: a theoretical analysis. J. Theor. Biol. 30, 235–248.CrossRefGoogle ScholarPubMed
Lankeit, J. (2016) A new approach toward boundedness in a two-dimensional parabolic chemotaxis system with singular sensitivity. Math. Methods Appl. Sci. 39, 394–404.CrossRefGoogle Scholar
Lankeit, J. & Winkler, M. (2017) A generalized solution concept for the Keller–Segel system with logarithmic sensitivity: global solvability for large nonradial data. NoDEA Nonlinear Diff. Equ. Appl. 24, Art. 49, 33 pp.Google Scholar
Li, H. (2018) Spiky steady states of a chemotaxis system with singular sensitivity. J. Dynam. Differ. Equ. 30, 1775–1795.CrossRefGoogle Scholar
Lin, C.-S., Ni, W.-M. & Takagi, I. (1988) Large amplitude stationary solutions to a chemotaxis system. J. Differ. Equ. 72, 1–27.CrossRefGoogle Scholar
Lin, F., Ni, W.-M. & Wei, J. (2007) On the number of interior peak solutions for a singularly perturbed Neumann problem. Comm. Pure Appl. Math. 60, 252–281.CrossRefGoogle Scholar
Liu, D. & Tao, Y. (2015) Global boundedness in a fully parabolic attraction-repulsion chemotaxis model. Math. Method Appl. Sci. 38, 2537–2546.CrossRefGoogle Scholar
Nagai, T., Senba, T. & Yoshida, K. (1997) Application of the Trudinger–Moser inequality to a parabolic system of chemotaxis. Funkcial. Ekvac. 40, 411–433.Google Scholar
Nanjundiah, V. (1973) Chemotaxis, signal relaying and aggregation morphology. J. Theor. Biol. 42, 63–105.CrossRefGoogle ScholarPubMed
Ni, W.-M. (2011) The Mathematics of Diffusion, CBMS-NSF Regional Conference Series in Applied Mathematics, Vol. 82. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, xii+110 pp.Google Scholar
Ni, W.-M. & Takagi, I. (1991) On the shape of least enery solutions to a semilinear Neumann problem. Comm. Pure Appl. Math. 44, 819–851.CrossRefGoogle Scholar
Ni, W.-M. & Takagi, I. (1993) Locating peaks of least energy solutions to a semilinear Neumann problem. Duke Math. J. 70, 247–281.CrossRefGoogle Scholar
Pejsachowicz, J. & Rabier, P. J. (1998) Degree theory for C 1 Fredholm mappings of index 0. J. Anal. Math. 76, 289–319.CrossRefGoogle Scholar
Pfeffer, W. (1883) Lokomotorische Richtungsbewegungen durch chemische reize. Ber. Deutsche Botan. Gesellschaft 1, 524–533.Google Scholar
Rabinowitz, P. (1971) Some global results for nonlinear eigenvalue problems. J. Funct. Anal. 7, 487–513.CrossRefGoogle Scholar
Schaaf, R. (1985) Stationary solutions of chemotaxis systems. Trans. Amer. Math. Soc. 292, 531–556.CrossRefGoogle Scholar
Schiller, R. (1976) Bacterial chemotaxis: a survey. Gen. Relat. Gravit. 7, 127–133.CrossRefGoogle Scholar
Shi, J. & Wang, X. (2009) On global bifurcation for quasilinear elliptic systems on bounded domains. J. Differ. Equ. 246, 2788–2812.CrossRefGoogle Scholar
Tao, Y., Wang, L. & Wang, Z.-A. (2013) Large-time behavior of a parabolic-parabolic chemotaxis model with logarithmic sensitivity in one dimension. Discrete Contin. Dyn. Syst. 18, 821–845.Google Scholar
Tso, W.-W. & Adler, J. (1974) Negative Chemotaxis in Escherichia coli. J. Bacteriol. 118, 560–576.CrossRefGoogle ScholarPubMed
Wang, Q. (2015) Boundary spikes of a Keller–Segel chemotaxis system with saturated logarithmic sensitivity. Discrete Contin. Dyn. Syst. Ser. B 20, 1231–1250.CrossRefGoogle Scholar
Wang, Q. (2015) Global solutions of a Keller–Segel system with saturated logarithmic sensitivity function. Commun. Pure Appl. Anal. 14, 383–396.CrossRefGoogle Scholar
Wang, Q., Yan, J. & Gai, C. (2016) Qualitative analysis of stationary Keller–Segel chemotaxis models with logistic growth. Z. Angew. Math. Phys. 67, Art. 51, 25 pp.CrossRefGoogle Scholar
Wang, Q., Yang, J. & Zhang, L. (2017) Time periodic and stable patterns of a two-competing-species Keller–Segel chemotaxis model: effect of cellular growth, Discrete Contin. Dyn. Syst. Ser. B, 22 (2017), 3547–3574.Google Scholar
Wang, Q., Zhang, L., Yang, J. & Hu, J. (2015) Global existence and steady states of a two competing species Keller–Segel chemotaxis model. Kinet. Relat. Models 8, 777–807.CrossRefGoogle Scholar
Wang, X. (2000) Qualitative behavior of solutions of chemotactic diffusion systems: effects of motility and chemotaxis and dynamics. SIAM J. Math. Anal. 31, 535–560.CrossRefGoogle Scholar
Wang, X. & Xu, Q. (2013) Spiky and transition layer steady states of chemotaxis systems via global bifurcation and Helly’s compactness theorem. J. Math. Biol. 66, 1241–1266.CrossRefGoogle ScholarPubMed
Wang, Z.-A. (2013) Mathematics of traveling waves in chemotaxis–Review paper. Discrete Contin. Dyn. Syst. Ser. B 18, 601–641.Google Scholar
Winkler, M. (2010) Aggregation vs. global diffusive behavior in the higher-dimensional Keller–Sege+l model. J. Differ. Equ. 248, 2889–2905.CrossRefGoogle Scholar
Zhang, Y., Chen, X., Hao, J., Lai, X. & Qin, C. (2017) Dynamics of spike in a Keller–Segel’s minimal chemotaxis model. Discrete Contin. Dyn. Syst. 37, 1109–1127.CrossRefGoogle Scholar