Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T06:30:32.222Z Has data issue: false hasContentIssue false
  • English
  • Français

A new class of costs for optimal transport planning

Part of: Miscellaneous topics in calculus of variations and optimal control Numerical methods in calculus of variations and optimal control Classical measure theory

Published online by Cambridge University Press:  29 November 2018

J.-J. ALIBERT ,
G. BOUCHITTÉ Open the ORCID record for G. BOUCHITTÉ [Opens in a new window]  and
T. CHAMPION
J.-J. ALIBERT
Affiliation:
Laboratoire IMATH, Université de Toulon, 83957 La Garde Cedex, France e-mails: alibert@univ-tln.fr; bouchitte@univ-tln.fr; champion@univ-tln.fr
G. BOUCHITTÉ*
Affiliation:
Laboratoire IMATH, Université de Toulon, 83957 La Garde Cedex, France e-mails: alibert@univ-tln.fr; bouchitte@univ-tln.fr; champion@univ-tln.fr
T. CHAMPION
Affiliation:
Laboratoire IMATH, Université de Toulon, 83957 La Garde Cedex, France e-mails: alibert@univ-tln.fr; bouchitte@univ-tln.fr; champion@univ-tln.fr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

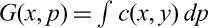We study a class of optimal transport planning problems where the reference cost involves a non-linear function G(x, p) representing the transport cost between the Dirac measure δx and a target probability p. This allows to consider interesting models which favour multi-valued transport maps in contrast with the classical linear case ($G(x,p)=\int c(x,y)dp$) where finding single-valued optimal transport is a key issue. We present an existence result and a general duality principle which apply to many examples. Moreover, under a suitable subadditivity condition, we derive a Kantorovich–Rubinstein version of the dual problem allowing to show existence in some regular cases. We also consider the well studied case of Martingale transport and present some new perspectives for the existence of dual solutions in connection with Γ-convergence theory.

Keywords

Optimal transportKantorovich-Rubinstein dualityMartingale constraint

MSC classification

Primary: 28A33: Spaces of measures, convergence of measures
Secondary: 49N05: Linear optimal control problems 49M29: Methods involving duality 90C46: Optimality conditions, duality
Type
Papers
Information
European Journal of Applied Mathematics , Volume 30 , Special Issue 6: Applied Optimal Transport , December 2019 , pp. 1229 - 1263
Copyright
© Cambridge University Press 2018 

References

Attouch, H. (1984) Variational Convergence for Functions and Operators. Pitman Applicable Mathematics Series, Advanced Publishing Program, Boston, MA.Google Scholar
Auslender, A. & Teboulle, M. (2003) Asymptotic Cones and Functions in Optimization and Variational Inequalities. Springer Monographs in Mathematics, Springer-Verlag, New York.Google Scholar
Beiglböck, M. & Griessler, C. (2014) An optimality principle with applications in optimal transport and its offspring. arXiv:1404.7054v2.Google Scholar
Beiglböck, M., Henry-Labordère, P. & Penkner, F. (2013) Model-independent bounds for option prices: a mass transport approach. Finance Stoch. 17(3), 477–501.CrossRefGoogle Scholar
Beiglböck, M. & Juillet, N. (2016) On a problem of optimal transport under marginal martingale constraints. Ann. Probab. 44(1), 42–106.CrossRefGoogle Scholar
Beiglböck, M., Lim, T. & Oblój, J. (2017). Dual attainment for the martingale transport problem. arXiv:1705.04273v1.Google Scholar
Beiglböck, M., Nutz, M. & Touzi, N. (2017) Complete duality for martingale optimal transport on the line. Ann. Probab. 45(5), 3038–3074.CrossRefGoogle Scholar
Castaing, C. & Valadier, M. (1977) Convex Analysis and Measurable Multifunctions. Lecture Notes in Mathematics, Vol. 580. Springer-Verlag, Berlin-New York.CrossRefGoogle Scholar
Gangbo, W. (1994) An elementary proof of the polar factorization of vector-valued functions. Arch. Ration. Mech. Anal. 128(4), 381–399.CrossRefGoogle Scholar
Ghoussoub, N., Kim, Y.-H. & Lim, T. (2016). Structure of optimal martingale transport plans in general dimensions. arXiv:1508.01806.Google Scholar
Gozlan, N., Roberto, C., Samson, P.-M. & Tetali, P. (2017) Kantorovich duality for general transport costs and applications. J. Funct. Anal. 273(11), 3327–3405.CrossRefGoogle Scholar
Hobson, D. & Neuberger, A. (2012) Robust bounds for forward start options. Math. Finance 22(1), 31–56.CrossRefGoogle Scholar
Juillet, N. (2016) Stability of the shadow projection and the left-curtain coupling. Ann. Inst. Henri Poincaré Probab. Stat. 52(4), 1823–1843.CrossRefGoogle Scholar
Marton, K. (1996) A measure concentration inequality for contracting Markov chains. Geom. Funct. Anal. 6(3), 556–571.CrossRefGoogle Scholar
Samson, P.-M. (2007) Infimum-convolution description of concentration properties of product probability measures, with applications. Ann. Inst. H. Poincaré Probab. Statist. 43(3), 321–338.CrossRefGoogle Scholar
Santambrogio, F. (2015) Optimal Transport for Applied Mathematicians: Calculus of Variations, PDEs, and Modeling. Progress in Nonlinear Differential Equations and Their Applications, Vol. 87, Birkhäuser/Springer, Cham.CrossRefGoogle Scholar
Strassen, V. (1965) The existence of probability measures with given marginals. Ann. Math. Statist. 36, 423–439.CrossRefGoogle Scholar
Villani, C. (2003) Topics in Optimal Transportation. Graduate Studies in Mathematics, Vol. 58, American Mathematical Society, Providence, RI.Google Scholar
Villani, C. (2009) Optimal Transport. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], Vol. 338, Springer-Verlag, Berlin. Old and new.CrossRefGoogle Scholar
Zaev, D. A. (2015) On the Monge-Kantorovich problem with additional linear constraints. Mat. Zametki 98(5), 664–683.Google Scholar