Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-10T14:25:19.289Z Has data issue: false hasContentIssue false
  • English
  • Français

On the global existence and qualitative behaviour of one-dimensional solutions to a model for urban crime

Part of: Equations of mathematical physics and other areas of application Partial differential equations Parabolic equations and systems

Published online by Cambridge University Press:  02 November 2021

NANCY RODRIGUEZ Open the ORCID record for NANCY RODRIGUEZ [Opens in a new window]  and
MICHAEL WINKLER
NANCY RODRIGUEZ
Affiliation:
CU Boulder, Department of Applied Mathematics, Engineering Center, ECOT 225 Boulder, CO 80309-0526, USA email: rodrign@colorado.edu
MICHAEL WINKLER
Affiliation:
Institut für Mathematik, Universität Paderborn, 33098 Paderborn, Germany email: michael.winkler@math.uni-paderborn.de
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the no-flux initial-boundary value problem for the cross-diffusive evolution system: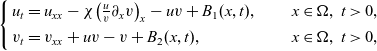

\begin{eqnarray*} \left\{ \begin{array}{ll} u_t = u_{xx} - \chi \big(\frac{u}{v} \partial_x v \big)_x - uv +B_1(x,t), \qquad & x\in \Omega, \ t>0, \\[1mm] v_t = v_{xx} +uv - v + B_2(x,t), \qquad & x\in \Omega, \ t>0, \end{array} \right. \end{eqnarray*}
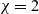which was introduced by Short et al. in [40] with $\chi=2$ to describe the dynamics of urban crime.

In bounded intervals 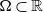$\Omega\subset\mathbb{R}$ and with prescribed suitably regular non-negative functions 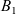$B_1$ and 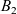$B_2$ , we first prove the existence of global classical solutions for any choice of 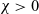$\chi>0$ and all reasonably regular non-negative initial data.

We next address the issue of determining the qualitative behaviour of solutions under appropriate assumptions on the asymptotic properties of 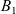$B_1$ and 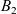$B_2$ . Indeed, for arbitrary 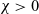$\chi>0$ , we obtain boundedness of the solutions given strict positivity of the average of 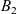$B_2$ over the domain; moreover, it is seen that imposing a mild decay assumption on 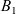$B_1$ implies that u must decay to zero in the long-term limit. Our final result, valid for all 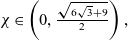$\chi\in\left(0,\frac{\sqrt{6\sqrt{3}+9}}{2}\right),$ which contains the relevant value 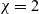$\chi=2$ , states that under the above decay assumption on 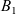$B_1$ , if furthermore 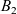$B_2$ appropriately stabilises to a non-trivial function 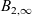$B_{2,\infty}$ , then (u,v) approaches the limit 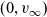$(0,v_\infty)$ , where 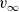$v_\infty$ denotes the solution of

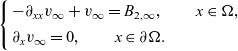\begin{eqnarray*} \left\{ \begin{array}{l} -\partial_{xx}v_\infty + v_\infty = B_{2,\infty}, \qquad x\in \Omega, \\[1mm] \partial_x v_{\infty}=0, \qquad x\in\partial\Omega. \end{array} \right. \end{eqnarray*}
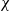We conclude with some numerical simulations exploring possible effects that may arise when considering large values of $\chi$ not covered by our qualitative analysis. We observe that when 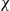$\chi$ increases, solutions may grow substantially on short time intervals, whereas only on large timescales diffusion will dominate and enforce equilibration.

Keywords

Urban crimeglobal existencedecay estimateslong-time behaviour

MSC classification

Primary: 35Q91: PDEs in connection with game theory, economics, social and behavioral sciences
Secondary: 35B40: Asymptotic behavior of solutions 35K55: Nonlinear parabolic equations
Type
Papers
Information
European Journal of Applied Mathematics , Volume 33 , Issue 5 , October 2022 , pp. 919 - 959
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahn, J., Kang, K. & Lee, J. (2021). Global well-posedness of logarithmic Keller-Segel type systems. J. Differ. Equ. 287, 185–211.CrossRefGoogle Scholar
Amann, H. (1989). Dynamic theory of quasilinear parabolic systems III. Global existence. Math. Z. 202, 219–250.Google Scholar
Barbaro, A. B. T., Chayes, L. & D’Orsogna, M. R. (2013). Territorial developments based on graffiti: A statistical mechanics approach. Phys. A Stat. Mech. Appl. 392(1), 252–270.CrossRefGoogle Scholar
Bellomo, N., Bellouquid, A., Tao, Y. & Winkler, M. (2015). Toward a mathematical theory of Keller-Segel models of pattern formation in biological tissues. Math. Mod. Meth. Appl. Sci. 25, 1663–1763.CrossRefGoogle Scholar
Berestycki, H. & Nadal, J.-P. (2010). Self-organised critical hot spots of criminal activity. Eur. J. Appl. Math. 21(4–5), 371–399.CrossRefGoogle Scholar
Berestycki, H., Rodríguez, N. & Ryzhik, L. (2013). Traveling wave solutions in a reaction-diffusion model for criminal activity. Multiscale Model. Simul. 11(4), 1097–1126.CrossRefGoogle Scholar
Berestycki, H., Wei, J. & Winter, M. (2014). Existence of symmetric and asymmetric spikes for a crime hotspot model. SIAM J. Math. Anal. 46(1), 691–719.CrossRefGoogle Scholar
Biler, P. (1999). Global solutions to some parabolic-elliptic systems of chemotaxis. Adv. Math. Sci. Appl. 9(1), 347–359.Google Scholar
Cantrell, R. S., Cosner, C. & Manásevich, R. (2012). Global bifurcation of solutions for crime modeling equations. SIAM J. Appl. Math. 44(3), 1340–1358.CrossRefGoogle Scholar
Chaturapruek, S., Breslau, J., Yazidi, D., Kolokolnikiv, T. & McCalla, S. (2013). Crime modeling with Levy flights. SIAM J. Appl. Math. 73(4), 1703–1720.CrossRefGoogle Scholar
Cohen, L. E. & Felson, M. (1979). Social change and crime rate trends: A routine activity approach. Amer. Soc. Rev. 44(4), 588–608.CrossRefGoogle Scholar
D’Orsogna, M. R. & Perc, M. (2015). Statistical physics of crime: A review. Phys. Life Rev. 12, 1–21.CrossRefGoogle ScholarPubMed
Espejo, E. & Winkler, M. (2018). Global classical solvability and stabilization in a two-dimensional chemotaxis-Navier-Stokes system modeling coral fertilization. Nonlinearity 31.CrossRefGoogle Scholar
Felson, M. (1987). Routine activities and crime prevention in the developing metropolis. Criminology 25, 911–932.CrossRefGoogle Scholar
Friedman, A. (1969). Partial Differential Equations. Holt, Rinehart & Winston, New York.Google Scholar
Gu, Y., Wang, Q. & Guangzeng, Y. (2017). Stationary patterns and their selection mechanism of Urban crime models with heterogeneous near–repeat victimization effect. Eur. J. Appl. Math. 21(1), 141–178.CrossRefGoogle Scholar
Henry, D. (1981). Geometric Theory of Semilinear Parabolic Equations. Springer Verlag, Berlin.CrossRefGoogle Scholar
Herrero, M. A. & VelÁzquez, J. J. L. (1997) A blow-up mechanism for a chemotaxis model. Ann. Scuola Normale Superiore Pisa 24, 633–683.Google Scholar
Hillen, T., Painter, K. J. & Winkler, M. (2013). Convergence of a cancer invasion model to a logistic chemotaxis model. Math. Models Meth. Appl. Sci. 23(01), 165–198.CrossRefGoogle Scholar
Horstmann, D. & Winkler, M. (2005) Boundedness vs. blow-up in a chemotaxis system. J. Differ. Equ. 215(1), 52–107.CrossRefGoogle Scholar
Johnson, S. D., Bowers, K. & Hirschfield, A. (1997). New insights into the spatial and temporal distribution of repeat victimisation. Br. J. Criminol. 37(2), 224–241.CrossRefGoogle Scholar
Jones, P. A., Brantingham, P. J. & Chayes, L. R. (2010). Statistical models of criminal behavior: The effects of law enforcement actions. Math. Models Methods Appl. Sci. 20(1), 1397–1423.CrossRefGoogle Scholar
Kelling, G. L. & Wilson, J. Q. (1982). Broken Windows.Google Scholar
Kolokolnikiv, T., Ward, M. J. & Wei, J. (2014). The stability of hotspot patterns for reaction-diffusion models of urban crime. DCDS-B 19, 1373–1410.CrossRefGoogle Scholar
Lankeit, J. (2016). A new approach toward boundedness in a two-dimensional parabolic chemotaxis system with singular sensitivity. Math. Meth. Appl. Sci. 39, 394–404.CrossRefGoogle Scholar
Lankeit, J. & Winkler, M. (2017). A generalized solution concept for the Keller–Segel system with logarithmic sensitivity: Global solvability for large nonradial data. Nonlinear Differ. Equ. Appl. 24(49), 24–49.CrossRefGoogle Scholar
Manásevich, R., Phan, Q. H. & Souplet, P. (2012). Global existence of solutions for a chemotaxis-type system arising in crime modelling. Eur. J. Appl. Math. 24(02), 273–296.CrossRefGoogle Scholar
McMillon, D., Simon, C. P. & Morenoff, J. (2014). Modeling the underlying dynamics of the spread of crime. PLoS ONE 9(4).CrossRefGoogle Scholar
Nagai, T. & Senaba, T. (1998). Global existence and blow-up of radial solutions to a parabolic-elliptic system of chemotaxis. Adv. Math. Sci. Appl. 8, 145–156.Google Scholar
Nagai, T. & Senaba, T. (2019). Facing low regularity in chemotaxis systems. Jahresber. Dtsch. Math. Ver. 123, 35–64.Google Scholar
Nuño, J. C., Herrero, M. A. & Primicerio, M. (2011). A mathematical model of a criminal-prone society. DCDS-S 4(1), 193–207.CrossRefGoogle Scholar
Osaki, K. & Yagi, A. (2001). Finite dimensional attractor for one-dimensional Keller-Segel equations. Funkcialaj Ekvacioj 22, 441–469.Google Scholar
Ricketson, L. (2010). A continuum model of residential burglary incorporating law enforcement. Preprint, 1–7.Google Scholar
Rodríguez, N. (2013). On the global well-posedness theory for a class of PDE models for criminal activity. Phys. D Nonlinear Phenom. 260(3), 191–200.CrossRefGoogle Scholar
Rodríguez, N. & Bertozzi, A. L. (2010). Local existence and uniqueness of solutions to a PDE model for criminal behavior. Math. Models Methods Appl. Sci. 20(Suppl. 01), 1425–1457.CrossRefGoogle Scholar
Rodríguez, N. & Ryzhik, L. (2016). Exploring the effects of social preference, economic disparity, and heterogeneous environments on segregation. Commun. Math. Sci. 14(2), 363–387.CrossRefGoogle Scholar
Rodrguez, N. & Winkler, M. (2020). Relaxation by nonlinear diffusion enhancement in a two-dimensional cross-diffusion model for urban crime propagation. Math. Models Methods Appl. Sci. 30(11), 2105–2137.CrossRefGoogle Scholar
Short, M. B., Bertozzi, A.L. & Brantingham, P. J. (2010). Nonlinear patterns in urban crime: Hotspots, bifurcations, and suppression. SIAM J. Appl. Dyn. Syst. 9(2), 462–483.CrossRefGoogle Scholar
Short, M. B., D’Orsogna, M. R., Brantingham, P. J. & Tita, G. E. (2009). Measuring and modeling repeat and near-repeat burglary effects. J. Quan. Criminol. 25(3), 325–339.CrossRefGoogle Scholar
Short, M. B., D’Orsogna, M. R., Pasour, V. B., Tita, G. E., Brantingham, P. J., Bertozzi, A.L. & Chayes, L. B. (2008). A statistical model of criminal behavior. Math. Models Methods Appl. Sci. 18(Suppl.), 1249–1267.CrossRefGoogle Scholar
Smith, L. M., Bertozzi, A. L., Brantingham, P. J., Tita, G. E. & Valasik, M. (2012). Adaptation of an animal territory model to street gang spatial patterns in Los Angeles. DCDS 32(9), 3223–3244.CrossRefGoogle Scholar
Stinner, C. & Winkler, M. (2011). Global weak solutions in a chemotaxis system with large singular sensitivity. Nonlinear Anal. Real World Appl. 12(6), 3727–3740.Google Scholar
Tao, Y. (2011). Boundedness in a chemotaxis model with oxygen consumption by bacteria. J. Math. Anal. Appl. 381(2), 521–529.CrossRefGoogle Scholar
Tao, Y. & Winkler, M. (2012). Eventual smoothness and stabilization of large-data solutions in a three-dimensional chemotaxis system with consumption of chemoattractant. J. Differ. Equ. 252(3), 2520–2543.CrossRefGoogle Scholar
Tao, Y. & Winkler, M. (2021). Global smooth solutions in a two-dimensional cross-diffusion system modeling propagation of urban crime. To appear in Communications in Mathematical Sciences.CrossRefGoogle Scholar
Tse, W. H. & Ward, M. J. (2016). Hotspot formation and dynamics for a continuum model of urban crime. Eur. J. Appl. Math., 583–624.CrossRefGoogle Scholar
Wang, Q., Wang, D. & Feng, Y. (2020). Global well-posedness and uniform boundedness of urban crime models: one-dimensional case. J. Differ. Equ. 269(7), 6216–6235.CrossRefGoogle Scholar
Winkler, M. (2002). A critical exponent in a degenerate parabolic equation. Math. Meth. Appl. Sci. 25, 911–925.CrossRefGoogle Scholar
Winkler, M. (2010). Absence of collapse in a parabolic chemotaxis system with signal-dependent sensitivity. Math. Nachr. 283(11), 1664–1673.CrossRefGoogle Scholar
Winkler, M. (2010). Aggregation vs. global diffusive behavior in the higher-dimensional Keller-Segel model. J. Differ. Equ. 248(12), 2889–2905.CrossRefGoogle Scholar
Winkler, M. (2011). Global solutions in a fully parabolic chemotaxis system with singular sensitivity. Math. Methods Appl. Sci. 34(2), 176–190.CrossRefGoogle Scholar
Winkler, M. (2013). Finite-time blow-up in the higher-dimensional parabolic-parabolic Keller-Segel system. J. Math. Pures Appl. 100, 748–767.CrossRefGoogle Scholar
Winkler, M. (2014). Stabilization in a two-dimensional chemotaxis-Navier-Stokes system. Arch. Rat. Mech. Anal. 211(2), 455–487.CrossRefGoogle Scholar
Winkler, M. (2019). A three-dimensional Keller-Segel-Navier-Stokes system with logistic source: Global weak solutions and asymptotic stabilization. J. Funct. Anal. 276(1), 1339–1401.CrossRefGoogle Scholar
Winkler, M. (2019). Global solvability and stabilization in a two-dimensional cross-diffusion system modeling urban crime propagation. Ann. Inst. Henri Poincare C, Anal. Non lineaire 36.Google Scholar
Zipkin, J., Short, M. B. & Bertozzi, A. L. (2014). Cops on the dots in a mathematical model of urban crime and police response. DCDS-B 19(0), 1479–1506.CrossRefGoogle Scholar