Article contents
A sharp interface limit of the phase field equations: one-dimensional and axisymmetric
Published online by Cambridge University Press: 26 September 2008
Abstract
We study the singular limit of the dimensionless phase-field equations
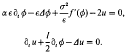
We consider two cases: either the space dimension is 1 and then ɛ tends to zero; or the solutions are radially symmetric and then both ɛ and α tend to zero. It turns out that, in the first case, the limiting functions solve the Stefan problem with kinetic undercooling, provided the initial temperature is small compared to the surface tension and the latent heat. In the second case, the limiting functions satisfy the Stefan problem coupled with the Gibbs–Thomson law for the melting temperature. We show, in addition, that the multiplicity of the interface is always one, in a sense to be explained at the end of § 1. As main tool we use energy type estimates, and prove that the formal first-order asymptotic expansion with respect to ɛ in fact gives an approximation of the exact solution. Our results hold without smoothness assumptions on the limiting Stefan problem.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Cambridge University Press 1996
References
- 11
- Cited by

